Question

（本小题共13分）

    已知椭圆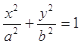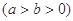和直线L: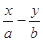=1, 椭圆的离心率，直线L与坐标原点的距离为。

（1）求椭圆的方程；

（2）已知定点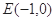，若直线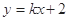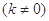与椭圆相交于C、D两点，试判断是否存在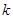值，使以CD为直径的圆过定点E？若存在求出这个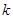值，若不存在说明理由。

 

Answer 1

【答案】

（1）+y²=1.（2）当=时以CD为直径的圆过定点E.

【解析】解：（1）直线L:=1,∴=.①      ．．．．．．．．．．．．．．．．．．1分

e=.②   ．．．．．．．．．．．．．．．．．．3分

   由①得

，3

     由②3得     ∴所求椭圆的方程是+y²=1. ．．．．．．．．．．5分

(2)联立得：.

Δ  ．．．．．．．．．．．．7分

设，则有

．．．．．．9分

 ∵，且以CD为圆心的圆点过点E，

 ∴EC⊥ED.                                       ．．．．．．．．．．．．．．．．．．11分

则

∴，解得=＞1,

∴当=时以CD为直径的圆过定点E.                ．．．．．．．．．．．．．．．．．．13分