题目内容
已知椭圆
解:设L′∥l且与椭圆有唯一公共点,L′:4x-5y+c=0,则由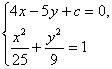
得25x2+8cx+c2-225=0.Δ=64c2-4×25(c2-225)=0,∴c=±25,c=-25(舍).∴L′:4x-5y+25=0.
设切点P(x0,y0),∴x0=-4,y0=![]() ,即椭圆上存在点P(-4,
,即椭圆上存在点P(-4,![]() ),到直线l的距离最小,最小值为分
),到直线l的距离最小,最小值为分 ![]() =
=![]() .
.

练习册系列答案
相关题目
题目内容
已知椭圆
解:设L′∥l且与椭圆有唯一公共点,L′:4x-5y+c=0,则由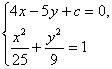
得25x2+8cx+c2-225=0.Δ=64c2-4×25(c2-225)=0,∴c=±25,c=-25(舍).∴L′:4x-5y+25=0.
设切点P(x0,y0),∴x0=-4,y0=![]() ,即椭圆上存在点P(-4,
,即椭圆上存在点P(-4,![]() ),到直线l的距离最小,最小值为分
),到直线l的距离最小,最小值为分 ![]() =
=![]() .
.
