题目内容
8.已知函数f(x)=lnx-ax2+ax恰有两个零点,则实数a的取值范围为( )| A. | (-∞,0) | B. | (0,+∞) | C. | (0,1)∪(1,+∞) | D. | (-∞,0)∪{1} |
分析 函数f(x)的定义域为(0,+∞),由题知方程 lnx-ax2+ax=0,即方程$\frac{lnx}{x}=a(x-1)$恰有两解.即两个函数有两个交点.利用导数研究函数的单调性极值与最值,即可得出.
解答 解:函数f(x)的定义域为(0,+∞),由题知方程 lnx-ax2+ax=0,即方程$\frac{lnx}{x}=a(x-1)$恰有两解.
设$g(x)=\frac{lnx}{x}$,则g'(x)=$\frac{1-lnx}{x^2}$,当0<x<e时,g'(x)>0,当x>e时,g'(x)<0,
∴g(x)在(0,e)上是增函数,在(e,+∞)上是减函数,且g(1)=0,当x>e时,g(x)>0,g'(1)=1,
作出函数y=g(x)与函数y=a(x-1)的图象如下图所示,
由图可知,函数y=g(x)的图象与函数y=a(x-1)的图象恰有2个交点的充要条件为0<a<1或a>1,
故选:C.
点评 本题考查了利用导数研究函数的单调性极值与最值,考查了转化能力与计算能力,属于难题.

练习册系列答案
相关题目
3.定义域为R的奇函数f(x)是减函数,当f(a)+f(a2)>0成立时,实数a的取值范围是( )
| A. | a<-1或a>0 | B. | -1<a<0 | C. | a<0或a>1 | D. | a<-1或a>1 |
13.在△ABC中,a,b,c分别是角A,B,C所对边的边长,若cosA+sinA-$\frac{2}{cosC+sinC}$=0,则$\frac{a+c}{b}$的值是( )
| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 1 |
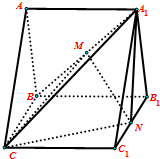 在直棱柱ABC-A1B1C1中,平面A1BC⊥平面A1ABB1,且AA1=AB=BC=2.M、N分别为A1B、B1C1中点.
在直棱柱ABC-A1B1C1中,平面A1BC⊥平面A1ABB1,且AA1=AB=BC=2.M、N分别为A1B、B1C1中点.