题目内容
4.若双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(0<a<b)的右支上存在一点,它到右焦点及到直线x=-$\frac{a^2}{c},({{c^2}={a^2}+{b^2}})$的距离相等,则离心率e的取值范围是( )| A. | $({1,\sqrt{2}})$ | B. | $({1,\sqrt{2}+1}]$ | C. | $({\sqrt{2},\sqrt{2}+1}]$ | D. | $[{\sqrt{2}+1,+∞})$ |
分析 由双曲线的定义可得 PF′-PF=2a,以及双曲线的第二定义得PF=$\frac{2a}{e-1}$=$\frac{2{a}^{2}}{c-a}$≥c-a,建立a,c的关系进行求解即可.
解答 解:设双曲线的右焦点F (c,0),左焦点F′(-c,0 ),
由双曲线的定义可得 PF′-PF=2a,以及圆锥曲线的第二定义得 $\frac{PF′}{PF}$=e,
∴ePF-PF=2a,
∴PF=$\frac{2a}{e-1}$=$\frac{2{a}^{2}}{c-a}$≥c-a,
∴$\frac{c}{a}$≤$\sqrt{2}$+1.
再由 e>1,∴1<e≤$\sqrt{2}$+1,
故选 B.
点评 本题考查双曲线的定义和标准方程,以及双曲线的简单性质的应用,利用双曲线的第二定义是解决本题的关键.综合性较强.

练习册系列答案
相关题目
19.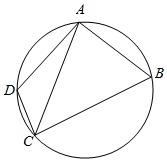 如图,圆内接四边形ABCD中,AB=2,BC=4,∠ABC=60° 顶点D在劣弧$\widehat{AC}$上运动,则三角形ACD面积的最大值等于( )
如图,圆内接四边形ABCD中,AB=2,BC=4,∠ABC=60° 顶点D在劣弧$\widehat{AC}$上运动,则三角形ACD面积的最大值等于( )
 如图,圆内接四边形ABCD中,AB=2,BC=4,∠ABC=60° 顶点D在劣弧$\widehat{AC}$上运动,则三角形ACD面积的最大值等于( )
如图,圆内接四边形ABCD中,AB=2,BC=4,∠ABC=60° 顶点D在劣弧$\widehat{AC}$上运动,则三角形ACD面积的最大值等于( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
13.执行如图所示的程序框图,若输出的n的值为7,则输入的T的最大值为( )


| A. | 339 | B. | 212 | C. | 190 | D. | 108 |