题目内容
2.已知不等式|x+2|+|x-2|<18的解集为A.(1)求A;
(2)若?a,b∈A,x∈(0,+∞),不等式a+b<x$+\frac{4}{x}$+m恒成立,求实数m的取值范围.
分析 (1)分x<-2,-2≤x≤2,x>2三种情况去绝对值符号将不等式转化为一元一次不等式求解;
(2)分别求出a+b和x$+\frac{4}{x}$+m的范围,令a+b的最大值小于x$+\frac{4}{x}$+m的最小值即可.
解答 解:(1)①当x<-2时,-x-2-x+2<18,解得-9<x<-2;
②当-2≤x≤2时,x+2-x+2<18,恒成立;
③当x>2时,x+2+x-2<18,解得2<x<9.
综上,不等式|x+2|+|x-2|<18的解集为(-9,-2)∪[-2,2]∪(2,9)=(-9,9).
∴A=(-9,9).
(2)∵a,b∈(-9,9),∴a+b∈(-18,18).∵a+b<x$+\frac{4}{x}$+m恒成立,
∴18≤x$+\frac{4}{x}$+m恒成立,∵x∈(0,+∞),∴x+$\frac{4}{x}$+m≥2$\sqrt{x•\frac{4}{x}}$+m=4+m.
∴18≤4+m,解得m≥14.
∴m的取值范围是[14,+∞).
点评 本题考查了绝对值不等式的解法,基本不等式的性质,函数恒成立问题,属于中档题.

练习册系列答案
相关题目
8.麦当劳店每天的房租、人员工资等固定成本为200元,某种食品每份的成本价是5元,销售单价与日均销售量的关系如下表所示:
请你根据以上数据作出分析,该麦当劳店怎样定价才能获得最大利润?
| 销售单价/元 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 日均销售量/份 | 440 | 400 | 360 | 320 | 280 | 240 | 200 |
6.将30.4,0.43,log43按从小到大的顺序排列,正确的是( )
| A. | 0.43<30.4<log43 | B. | log43<0.43<30.4 | C. | 0.43<log43<30.4 | D. | log43<30.4<0.43 |
7.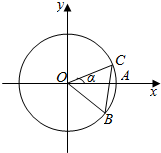 如图,圆O与x轴的正半轴的交点为A,点C、B在圆O上,且点C位于第一象限,点B的坐标为($\frac{12}{13}$,-$\frac{5}{13}$),∠AOC=α,若|BC|=1,则$\sqrt{3}$cos2$\frac{α}{2}$-sin$\frac{α}{2}$cos$\frac{α}{2}$-$\frac{\sqrt{3}}{2}$的值为( )
如图,圆O与x轴的正半轴的交点为A,点C、B在圆O上,且点C位于第一象限,点B的坐标为($\frac{12}{13}$,-$\frac{5}{13}$),∠AOC=α,若|BC|=1,则$\sqrt{3}$cos2$\frac{α}{2}$-sin$\frac{α}{2}$cos$\frac{α}{2}$-$\frac{\sqrt{3}}{2}$的值为( )
 如图,圆O与x轴的正半轴的交点为A,点C、B在圆O上,且点C位于第一象限,点B的坐标为($\frac{12}{13}$,-$\frac{5}{13}$),∠AOC=α,若|BC|=1,则$\sqrt{3}$cos2$\frac{α}{2}$-sin$\frac{α}{2}$cos$\frac{α}{2}$-$\frac{\sqrt{3}}{2}$的值为( )
如图,圆O与x轴的正半轴的交点为A,点C、B在圆O上,且点C位于第一象限,点B的坐标为($\frac{12}{13}$,-$\frac{5}{13}$),∠AOC=α,若|BC|=1,则$\sqrt{3}$cos2$\frac{α}{2}$-sin$\frac{α}{2}$cos$\frac{α}{2}$-$\frac{\sqrt{3}}{2}$的值为( )| A. | $\frac{5}{13}$ | B. | $\frac{12}{13}$ | C. | -$\frac{5}{13}$ | D. | -$\frac{12}{13}$ |



