题目内容
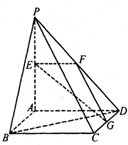 如图,P为正方形ABCD所在平面外一点PA⊥平面ABCD,且PA=AD=2,E、F、G分别是线段PA、PD、CD的中点.
如图,P为正方形ABCD所在平面外一点PA⊥平面ABCD,且PA=AD=2,E、F、G分别是线段PA、PD、CD的中点.(I)求证:EF∥平面ABCD;
(II)求证:平面PBC∥平面EFG;
(III)求异面直线EG与BD所成角的大小.
分析:(I)要证线面平行,根据线面平行的判定定理,只要证明平面外的直线平行于平面内的一条直线即可;
(II)要证面面平行,可根据面面平行的判定定理,利用一个平面内的两条相交直线分别平行于另一平面内的两条相交直线即可;
(III)建立空间直角坐标系,将求异面直线EG与BD所成的角的余弦值问题,转化为向量夹角的余弦值即可.
(II)要证面面平行,可根据面面平行的判定定理,利用一个平面内的两条相交直线分别平行于另一平面内的两条相交直线即可;
(III)建立空间直角坐标系,将求异面直线EG与BD所成的角的余弦值问题,转化为向量夹角的余弦值即可.
解答: 证明:(I)∵E,F分别是线段AP,PD的中点,
证明:(I)∵E,F分别是线段AP,PD的中点,
∴EF∥AD
∵AD?平面ABCD,EF?平面ABCD
∴EF∥平面ABCD;
(II)∵E,F,G分别是线段PA,PD,CD的中点,
∴FG∥PC,EF∥AD
在正方形ABCD中,∵AD∥BC,∴EF∥BC
∵PC?平面PBC,BC?平面PBC,PC∩BC=C
EF?平面EFG,FG?平面EFG,EF∩FG=F
∴平面PBC∥平面EFG;
(III)建立如图所示的空间直角坐标系A-xyz,
则B(2,0,0),D(0,2,0),E(0,0,1),G(1,2,0).
∴
=(1,2,-1),
=(-2,2,0),
∴cos<
,
>=
=
=
,
∴异面直线EG与BD所成角的大小为arccos
.
 证明:(I)∵E,F分别是线段AP,PD的中点,
证明:(I)∵E,F分别是线段AP,PD的中点,∴EF∥AD
∵AD?平面ABCD,EF?平面ABCD
∴EF∥平面ABCD;
(II)∵E,F,G分别是线段PA,PD,CD的中点,
∴FG∥PC,EF∥AD
在正方形ABCD中,∵AD∥BC,∴EF∥BC
∵PC?平面PBC,BC?平面PBC,PC∩BC=C
EF?平面EFG,FG?平面EFG,EF∩FG=F
∴平面PBC∥平面EFG;
(III)建立如图所示的空间直角坐标系A-xyz,
则B(2,0,0),D(0,2,0),E(0,0,1),G(1,2,0).
∴
| EG |
| BD |
∴cos<
| EG |
| BD |
| ||||
|
|
| -2+4 | ||||
|
| ||
| 6 |
∴异面直线EG与BD所成角的大小为arccos
| ||
| 6 |
点评:本题以线面垂直为载体,考查线面平行,面面平行,考查线线角,解题时正确运用线面平行、面面平行的判定定理是解题的关键.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
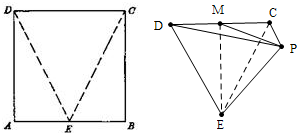 如图,ABCD是正方形,E是AB的中点,如将△DAE和△CBE分别沿虚线DE和CE折起,使AE与BE重合,记A与B重合后的点为P,则面PCD与面ECD所成的二面角为
如图,ABCD是正方形,E是AB的中点,如将△DAE和△CBE分别沿虚线DE和CE折起,使AE与BE重合,记A与B重合后的点为P,则面PCD与面ECD所成的二面角为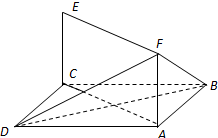 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直, 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直, (2011•揭阳一模)如图①边长为1的正方形ABCD中,点E、F分别为AB、BC的中点,将△BEF剪去,将△AED、△DCF分别沿DE、DF折起,使A、C两点重合于点P得一三棱锥如图②示.
(2011•揭阳一模)如图①边长为1的正方形ABCD中,点E、F分别为AB、BC的中点,将△BEF剪去,将△AED、△DCF分别沿DE、DF折起,使A、C两点重合于点P得一三棱锥如图②示.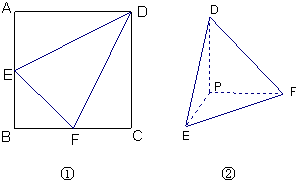 (2011•揭阳一模)如图①边长为1的正方形ABCD中,点E、F分别为AB、BC的中点,将△BEF剪去,将△AED、△DCF分别沿DE、DF折起,使A、C两点重合于点P得一三棱锥如图②示.
(2011•揭阳一模)如图①边长为1的正方形ABCD中,点E、F分别为AB、BC的中点,将△BEF剪去,将△AED、△DCF分别沿DE、DF折起,使A、C两点重合于点P得一三棱锥如图②示.