Question

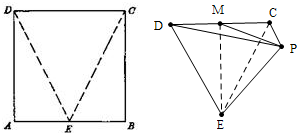如图，ABCD是正方形，E是AB的中点，如将△DAE和△CBE分别沿虚线DE和CE折起，使AE与BE重合，记A与B重合后的点为P，则面PCD与面ECD所成的二面角为

 

度．

Answer 1

分析：二面角的度量关键在于作出它的平面角，取CD的中点M，连接PM、EM，因为PD=PC，所以PM⊥CD；同理因为ED=EC，所以EM⊥CD，故∠PME即为面PCD与面ECD所成二面角的平面角．

解答：解：设正方形的边长为2，
取CD的中点M，连接PM、EM，
∵PD=PC，
∴PM⊥CD
∵ED=EC，
∴EM⊥CD
故∠PME即为面PCD与面ECD所成二面角的平面角．
在△PME中：PE=1，PM=

3

，EM=2，
∴cos∠PME=

PM2+ME2-PE2

2PM•ME

=

3

2

∴∠PME=30°
故答案为：30．

点评：本小题主要考查棱锥的结构特征，二面角和线面关系等基本知识，同时考查空间想象能力和推理、运算能力．