Question

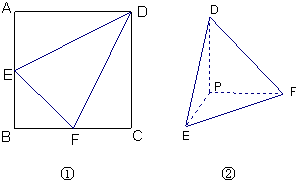（2011•揭阳一模）如图①边长为1的正方形ABCD中，点E、F分别为AB、BC的中点，将△BEF剪去，将△AED、△DCF分别沿DE、DF折起，使A、C两点重合于点P得一三棱锥如图②示．
（1）求证：PD⊥EF；
（2）求三棱锥P-DEF的体积；
（3）求点E到平面PDF的距离．

Answer 1

分析：（1）证明PD⊥EF，只需证明PD⊥平面PEF即可；
（2）解法1：依题意知图1中AE=CF=

1

2

，从而PE=PF=

1

2

，证明PE⊥PF，利用VP-DEF=VD-PEF=

1

3

S△PEF•PD可求；
解法2：依题意知图2中AE=CF=

1

2

，从而PE=PF=

1

2

，取EF的中点M，连接PM，则PM⊥EF，利用VP-DEF=VD-PEF=

1

3

S△PEF•PD可求；
（3）由（2）知PE⊥平面PDF，从而线段PE的长就是点E到平面PDF的距离．

解答：（1）证明：依题意知图1折前AD⊥AE，CD⊥CF，-------------------------------（1分）
∴PD⊥PE，PF⊥PD，-------------------------------------------------------（2分）
∵PE∩PF=P，∴PD⊥平面PEF-----------------------------------（4分）
又∵EF?平面PEF，∴PD⊥EF----------------------------------------（5分）
（2）解法1：依题意知图1中AE=CF=

1

2

，∴PE=PF=

1

2

，
在△BEF中，EF=

2

BE=

2

2

，-----（6分）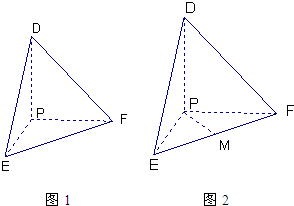
在△PEF中，PE²+PF²=EF²，
∴S△PEF=

1

2

•PE•PF=

1

2

•

1

2

•

1

2

=

1

8

------（8分）
∴VP-DEF=VD-PEF=

1

3

S△PEF•PD=

1

3

×

1

8

×1=

1

24

．-----（10分）
解法2：依题意知图2中AE=CF=

1

2

，∴PE=PF=

1

2

，
在△BEF中EF=

2

BE=

2

2

，------------------（6分）
取EF的中点M，连接PM
则PM⊥EF，∴PM=

PE2-EM2

=

2

4

---------（7分）
∴S△PEF=

1

2

EF•PM=

1

2

×

2

2

×

2

4

=

1

8

---------------（8分）
∴VP-DEF=VD-PEF=

1

3

S△PEF•PD=

1

3

×

1

8

×1=

1

24

．------------------------------（10分）
（3）由（2）知PE⊥PF，又PE⊥PD，∴PE⊥平面PDF---------------------（12分）
∴线段PE的长就是点E到平面PDF的距离--------------------------------------（13分）
∵PE=

1

2

，∴点E到平面PDF的距离为

1

2

．-------------------------------------（14分）

点评：本题考查线线垂直，考查三棱锥的体积，考查点面距离的计算，解题的关键是利用线面垂直证明线线垂直，掌握转换底面求体积．