题目内容
（1）已知A（1，2），B（3，-6），向量
，若 
，求x，y的值；
（2）向量
互相垂直，其中
．求sinθ，cosθ的值．
解：（1）由A（1，2），B（3，-6），得 
，则
，
又，且
所以
，解得：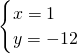
；
（2）由向量互相垂直，
则
，
即sinθ=2cosθ，
又sin2θ+cos2θ=1，，
解得：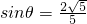
，
．
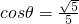分析：（1）由给出的A（1，2），B（3，-6），求出向量
，结合 ，直接利用向量平行的坐标表示列式求解即可；
（2）由向量
互相垂直，其数量积等于0，联立sin2θ+cos2θ=1，则可求给定范围内的sinθ，cosθ的值．
点评：本题综合考查了平面向量的坐标表示，考查了共线向量与垂直向量，向量共线与垂直的坐标表示是高考常考查的知识点，记忆时容易混淆．此题是基础题．
，则，又
，且 所以
，解得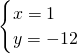：；（2）由向量
互相垂直，则
，即sinθ=2cosθ，
又sin2θ+cos2θ=1，
，解得：
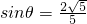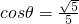，．分析：（1）由给出的A（1，2），B（3，-6），求出向量
，结合 ，直接利用向量平行的坐标表示列式求解即可；（2）由向量
互相垂直，其数量积等于0，联立sin2θ+cos2θ=1，则可求给定范围内的sinθ，cosθ的值．点评：本题综合考查了平面向量的坐标表示，考查了共线向量与垂直向量，向量共线与垂直的坐标表示是高考常考查的知识点，记忆时容易混淆．此题是基础题．
练习册系列答案
中考利剑中考试卷汇编系列答案
教育世家状元卷系列答案
黄冈课堂作业本系列答案
单元加期末复习先锋大考卷系列答案
相关题目