题目内容
某海滨浴场的岸边可以近似的看成直线,位于岸边A处的救生员发现海
中B处有人求救,救生员没有直接从A处游向B处,而是沿岸边自A跑到距离B最近的D
处,然后游向B处.若救生员在岸边的行进速度是6米/秒,在海中的行进速度是2米/秒.
(不考虑水流速度等因素)

(1)请分析救生员的选择是否正确;
(2)在AD上找一点C,使救生员从A到B的时间最短,并求出最短时间.
中B处有人求救,救生员没有直接从A处游向B处,而是沿岸边自A跑到距离B最近的D
处,然后游向B处.若救生员在岸边的行进速度是6米/秒,在海中的行进速度是2米/秒.
(不考虑水流速度等因素)

(1)请分析救生员的选择是否正确;
(2)在AD上找一点C,使救生员从A到B的时间最短,并求出最短时间.
(1)救生员的选择是正确的(2)

(1)本小题要计算出从A处游向B处的时间 ,再计算出沿岸边自A跑到距离B最近的D处,然后游向B处所用时间
,再计算出沿岸边自A跑到距离B最近的D处,然后游向B处所用时间 ,如果
,如果 ,则说明选择正确,否则选择错误.
,则说明选择正确,否则选择错误.
(2)设CD=x,则AC=300-x, ,从而得到救生员从A经C到B的时间
,从而得到救生员从A经C到B的时间 ,再利用导数求其最值.
,再利用导数求其最值.
解:(1)从A处游向B处的时间 ,
,
而沿岸边自A跑到距离B最近的D处,然后游向B处的时间
而 ,所以救生员的选择是正确的. ……4分
,所以救生员的选择是正确的. ……4分
(2)设CD=x,则AC=300-x, ,使救生员从A经C到B的时间
,使救生员从A经C到B的时间
 ……………………6分
……………………6分
 ,令
,令
又 , ……………………9分
, ……………………9分
知 ……………………11分
……………………11分
答:(略) …………………12分
 ,再计算出沿岸边自A跑到距离B最近的D处,然后游向B处所用时间
,再计算出沿岸边自A跑到距离B最近的D处,然后游向B处所用时间 ,如果
,如果 ,则说明选择正确,否则选择错误.
,则说明选择正确,否则选择错误.(2)设CD=x,则AC=300-x,
 ,从而得到救生员从A经C到B的时间
,从而得到救生员从A经C到B的时间 ,再利用导数求其最值.
,再利用导数求其最值.解:(1)从A处游向B处的时间
 ,
,而沿岸边自A跑到距离B最近的D处,然后游向B处的时间

而
 ,所以救生员的选择是正确的. ……4分
,所以救生员的选择是正确的. ……4分(2)设CD=x,则AC=300-x,
 ,使救生员从A经C到B的时间
,使救生员从A经C到B的时间 ……………………6分
……………………6分 ,令
,令
又
 , ……………………9分
, ……………………9分知
 ……………………11分
……………………11分答:(略) …………………12分

练习册系列答案
相关题目
 中,
中, 的对边分别为
的对边分别为 且
且 成等差数列.(1)求
成等差数列.(1)求 的值;(2)求
的值;(2)求 的取值范围。
的取值范围。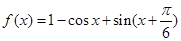 .
. 的最小正周期;
的最小正周期; 得内角
得内角 的对应边为
的对应边为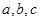 ,若
,若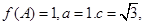 求
求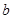 的值.
的值.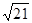 ,b=4,且BC边上的高h=
,b=4,且BC边上的高h=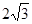 。
。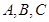 ,下列结论正确的个数是( )
,下列结论正确的个数是( )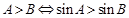 ;②
;②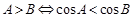 ③
③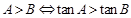
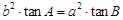 ,那么△ ABC一定是( )
,那么△ ABC一定是( ) 中,A=300,AB="4," BC="2" 则
中,A=300,AB="4," BC="2" 则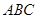 中,内角
中,内角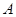 、
、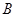 、
、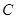 的对边分别为
的对边分别为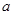 、
、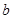 、
、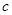 ,已知
,已知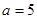 ,
,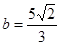 ,
,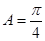 ,则
,则 。
。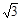 ,AB=2,则△ABC的面积为_________.
,AB=2,则△ABC的面积为_________.