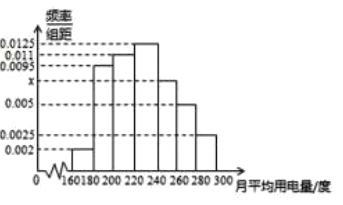
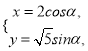题目内容
【题目】已知函数f(x2﹣1)=loga ![]() (a>0且a≠1)
(a>0且a≠1)
(1)求函数f(x)的解析式,并判断f(x)的奇偶性;
(2)解关于x的方程f(x)=loga ![]() .
.
【答案】
(1)解:∵f(x2﹣1)=loga ![]() =loga
=loga ![]() ,
,
∴ ![]() ,x∈(﹣1,1),
,x∈(﹣1,1),
又∵f(﹣x)+ ![]() +loga
+loga ![]() =0;
=0;
则f(x)是奇函数
(2)解:方程f(x)=loga ![]() 可化为
可化为 ![]() x=1;
x=1;
解得, ![]()
【解析】(1)化简f(x2﹣1)=loga ![]() =loga
=loga ![]() ,从而得
,从而得 ![]() ,x∈(﹣1,1),再判断f(﹣x)与f(x)的关系即可;(2)方程f(x)=loga
,x∈(﹣1,1),再判断f(﹣x)与f(x)的关系即可;(2)方程f(x)=loga ![]() 可化为
可化为 ![]() x=1;从而解得.
x=1;从而解得.
【考点精析】通过灵活运用函数的奇偶性,掌握偶函数的图象关于y轴对称;奇函数的图象关于原点对称即可以解答此题.

练习册系列答案
相关题目