题目内容
【题目】已知椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() ,短轴的两个端点分别为
,短轴的两个端点分别为![]() .
.
(Ⅰ)若![]() 为等边三角形,求椭圆
为等边三角形,求椭圆![]() 的方程;
的方程;
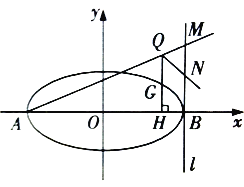
(Ⅱ)若椭圆![]() 的短轴长为
的短轴长为![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(Ⅰ)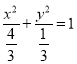 ;(Ⅱ)
;(Ⅱ)![]() 或
或![]() .
.
【解析】试题分析:(1)由![]() 为等边三角形可得a=2b,又c=1,集合
为等边三角形可得a=2b,又c=1,集合![]() 可求
可求![]() ,则椭圆C的方程可求;(2)由给出的椭圆C的短轴长为2,结合c=1求出椭圆方程,分过点F2的直线l的斜率存在和不存在讨论,当斜率存在时,把直线方程和椭圆方程联立,由根与系数关系写出两个交点的横坐标的和,把
,则椭圆C的方程可求;(2)由给出的椭圆C的短轴长为2,结合c=1求出椭圆方程,分过点F2的直线l的斜率存在和不存在讨论,当斜率存在时,把直线方程和椭圆方程联立,由根与系数关系写出两个交点的横坐标的和,把
![]() 转化为数量积等于0,代入坐标后可求直线的斜率,则直线l的方程可求
转化为数量积等于0,代入坐标后可求直线的斜率,则直线l的方程可求
试题解析:(1)![]() 为等边三角形,则
为等边三角形,则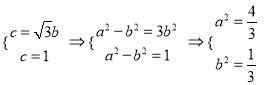 ……2
……2
椭圆![]() 的方程为:
的方程为: ![]() ; ……3
; ……3
(2)容易求得椭圆![]() 的方程为
的方程为![]() , ……5
, ……5
当直线![]() 的斜率不存在时,其方程为
的斜率不存在时,其方程为![]() ,不符合题意; ……6
,不符合题意; ……6
当直线的斜率存在时,设直线![]() 的方程为
的方程为![]() ,
,
由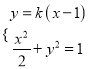 得
得![]() ,设
,设![]() ,
,
则![]() , ……8
, ……8
![]() ∵
∵![]() ,
,
∴![]() ,
,
即![]()
![]() ……10
……10
解得![]() ,即
,即![]() ,
,
故直线![]() 的方程为
的方程为![]() 或
或![]() . ……12
. ……12

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目