题目内容
已知函数 和
和 的图像关于原点对称,且
的图像关于原点对称,且 .
.
(1)求 的表达式;
的表达式;
(2)若 在
在 上是增函数,求实数
上是增函数,求实数 的取值范围.
的取值范围.
 和
和 的图像关于原点对称,且
的图像关于原点对称,且 .
.(1)求
 的表达式;
的表达式;(2)若
 在
在 上是增函数,求实数
上是增函数,求实数 的取值范围.
的取值范围.(1) ;(2)
;(2) .
.
 ;(2)
;(2) .
.试题分析:(1)设函数的图象上任意一点
 关于原点的对称点为
关于原点的对称点为 ,利用函数
,利用函数 和
和 的图象关于原点对称,可求得对称点之间的坐标关系,利用
的图象关于原点对称,可求得对称点之间的坐标关系,利用 ,可求函数
,可求函数 的解析式;
的解析式;(2)
 ,其对称轴方程为
,其对称轴方程为 ,利用
,利用 在
在 上是增函数,可求实数
上是增函数,可求实数 的取值范围.
的取值范围.(1)设函数
 的图象上任意一点
的图象上任意一点 关于原点的对称点为
关于原点的对称点为 ,则
,则 即
即 因为点
因为点 在函数
在函数 的图象上,所以
的图象上,所以 ,即
,即 ,故
,故 .
.(2)

①当
 时,
时, 在
在 上是增函数,
上是增函数,
②当
 时,对称轴的方程为
时,对称轴的方程为 .
.ⅰ)当
 时,
时, ,解得
,解得 .
.ⅱ)当
 时,
时, ,解得
,解得 .
.综上,
 .
.
练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
 ,且
,且 ,
, .
. 的解析式;
的解析式;
 (a≠0)满足
(a≠0)满足 ,
, 为偶函数,且x=-2是函数
为偶函数,且x=-2是函数 的一个零点.又
的一个零点.又 (
( >0).
>0).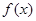 的解析式;
的解析式; 在
在 上有解,求实数
上有解,求实数 ,求
,求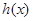 的单调区间.
的单调区间.
 的零点,则[x0]等于________.
的零点,则[x0]等于________. 满足对任意
满足对任意 ,均有
,均有 且
且 ,若方程
,若方程 恰有5个实数解,则实数
恰有5个实数解,则实数 的取值范围是 .
的取值范围是 . 对称。据此可推测对任意的非0实数a、b、c、m、n、g关于x的方程m[f(x)]2+n f(x)+g=0的解集不可能是( )
对称。据此可推测对任意的非0实数a、b、c、m、n、g关于x的方程m[f(x)]2+n f(x)+g=0的解集不可能是( ) ,
, ,若
,若 ,则
,则 ( )
( )