题目内容

斜率为1的直线经过抛物线y2=4x的焦点，与抛物线相交于两点A、B，求线段AB的长.

解：如下图，由抛物线的标准方程可知，焦点F（1，0），准线方程x=-1.

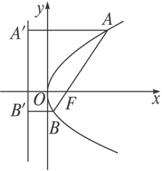
由题设，直线AB的方程为：y=x-1.

代入抛物线方程y2=4x，整理得：x2-6x+1=0.

解上述方程得：x1=3+2,x2=3-2,

分别代入直线方程得：y1=2+2,y2=2-2,

即A、B坐标分别为（3+2，2+2）、（3-2，2-2）.

∴|AB|==8.

练习册系列答案
相关题目
斜率为1的直线经过抛物线y2=4x的焦点，与抛物线相交于A，B两点，则|AB|=
 
．
已知抛物线C的参数方程为
x=8t2
y=8t
（t为参数），若斜率为1的直线经过抛物线C的焦点，且与圆（x-4）2+y2=r2（r＞0）相切，则r=
 
．
已知抛物线C1的参数方程为
x=8t2
y=8t
（t为参数），圆C2的极坐标方程为ρ=r（r＞0），若斜率为1的直线经过抛物线C1的焦点，且与圆C2相切，则r=（　　）
（1）（不等式选讲选做题）若关于x的不等式|x-1|+|x+m|＞3的解集为R，则实数m的取值范围是
（-∞，-4）∪（2，+∞）
（-∞，-4）∪（2，+∞）
．
（2）（坐标系与参数方程选做题）已知抛物线C1的参数方程为
x=8t2
y=8t
（t为参数），圆C2的极坐标方程为ρ=r（r＞0），若斜率为1的直线经过抛物线C1的焦点，且与圆C2相切，则r=
2
2
．

(1)(不等式选讲选做题)若关于x的不等式|x－1|＋|x＋m|>3的解集为R，则实数m的取值范围是________．

(2)(坐标系与参数方程选做题)已知抛物线C1的参数方程为(t为参数)，圆C2的极坐标方程为ρ＝r(r>0)，若斜率为1的直线经过抛物线C1的焦点，且与圆C2相切，则r＝________.

 

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网