题目内容
(1)(不等式选讲选做题)若关于x的不等式|x-1|+|x+m|>3的解集为R,则实数m的取值范围是
(2)(坐标系与参数方程选做题)已知抛物线C1的参数方程为
(t为参数),圆C2的极坐标方程为ρ=r(r>0),若斜率为1的直线经过抛物线C1的焦点,且与圆C2相切,则r=
.
(-∞,-4)∪(2,+∞)
(-∞,-4)∪(2,+∞)
.(2)(坐标系与参数方程选做题)已知抛物线C1的参数方程为
|
| 2 |
| 2 |
分析:(1)利用绝对值的几何意义可得,若使不等式|x-1|+|x+m|>3的解集为R,只需数轴上点A(其坐标为1)与点B(其坐标为-m)之间的距离大于3即可;
(2)抛物线C1的参数方程化为普通方程,确定焦点坐标为(2,0),从而可得直线方程;圆C2的极坐标方程为ρ=r(r>0),表示以原点为圆心,r为半径的圆,利用斜率为1的直线经过抛物线C1的焦点,且与圆C2相切,即可求得圆的半径.
(2)抛物线C1的参数方程化为普通方程,确定焦点坐标为(2,0),从而可得直线方程;圆C2的极坐标方程为ρ=r(r>0),表示以原点为圆心,r为半径的圆,利用斜率为1的直线经过抛物线C1的焦点,且与圆C2相切,即可求得圆的半径.
解答:解:(1)设数轴上点A的坐标为1,点B的坐标为-m,|AB|=|1+m|,
∵不等式|x-1|+|x+m|>3的解集为R,
∴|1+m|>3,
∴m<-4或m>2;
(2)抛物线C1的参数方程为
(t为参数),则普通方程为y2=8x,焦点坐标为(2,0);圆C2的极坐标方程为ρ=r(r>0),表示以原点为圆心,r为半径的圆
∵斜率为1的直线经过抛物线C1的焦点,且与圆C2相切,
∴直线y=x-2与圆C2相切
∴圆心到直线的距离为d=
=
∴圆的半径r=
故答案为:(-∞,-4)∪(2,+∞);
.
∵不等式|x-1|+|x+m|>3的解集为R,
∴|1+m|>3,
∴m<-4或m>2;
(2)抛物线C1的参数方程为
|
∵斜率为1的直线经过抛物线C1的焦点,且与圆C2相切,
∴直线y=x-2与圆C2相切
∴圆心到直线的距离为d=
| 2 | ||
|
| 2 |
∴圆的半径r=
| 2 |
故答案为:(-∞,-4)∪(2,+∞);
| 2 |
点评:本题(1)考查绝对值不等式,理解绝对值的几何意义是关键;(2)考查坐标系与参数方程,正确运用直线与圆相切是关键.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案
相关题目
 A.(不等式选讲选做题)如果存在实数x使不等式|x+1|-|x-2|<k成立,则实数k的取值范围是
A.(不等式选讲选做题)如果存在实数x使不等式|x+1|-|x-2|<k成立,则实数k的取值范围是 ,则线段CD的长为 .
,则线段CD的长为 .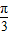 )的直角坐标是 .
)的直角坐标是 .
 ,则AC的长为 .
,则AC的长为 .