题目内容
19.已知$tanx=\frac{1}{3}$,则sinxcosx+1等于( )| A. | $\frac{13}{10}$ | B. | $-\frac{13}{10}$ | C. | $\frac{10}{13}$ | D. | $-\frac{10}{13}$ |
分析 由条件利用同角三角函数的基本关系,求得要求式子的值.
解答 解:∵$tanx=\frac{1}{3}$,则sinxcosx+1=$\frac{sinxcosx}{{sin}^{2}x{+cos}^{2}x}$+1=$\frac{tanx}{{tan}^{2}x+1}$+1=$\frac{\frac{1}{3}}{\frac{1}{9}+1}$+1=$\frac{13}{10}$,
故选:A.
点评 本题主要考查同角三角函数的基本关系的应用,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.若集合A={0,1,2,4},B={1,2,3},则A∪B=( )
| A. | {1,2} | B. | {0,3,4} | C. | {0,1,2,3,4} | D. | {0,1,1,2,2,3,4} |
14.cos420°+sin330°等于( )
| A. | 1 | B. | -1 | C. | $\frac{1}{2}$ | D. | 0 |
11.已知函数f(x)=x2-2|x-a|(a∈R).
(I)当a=0时,求方程f(x)=0的根;
(Ⅱ)当a>0时,若对任意的x∈[0,+∞),不等式f(x-1)≥2f(x)恒成立,求实数a的取值范围.
(I)当a=0时,求方程f(x)=0的根;
(Ⅱ)当a>0时,若对任意的x∈[0,+∞),不等式f(x-1)≥2f(x)恒成立,求实数a的取值范围.
8.函数$f(x)={x^2}(x-\frac{2}{x})$的导函数f′(x),则f′(1)等于( )
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
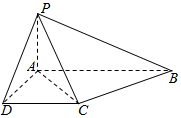 在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AB∥CD,且PA=AD=CD=a,AB=2a.求:
在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AB∥CD,且PA=AD=CD=a,AB=2a.求: