题目内容
7.当x∈[1,2]时,不等式2x-log${\;}_{\frac{1}{2}}$x+m≤0恒成立,则实数m的取值范围是(-∞,-5].分析 把不等式2x-log${\;}_{\frac{1}{2}}$x+m≤0变形为2x+log2x≤-m,令f(x)=2x+log2x,则f(x)在[1,2]上为增函数,求其最大值后可得-m的范围,进一步得到实数m的取值范围.
解答 解:当x∈[1,2]时,不等式2x-log${\;}_{\frac{1}{2}}$x+m≤0,
即2x+log2x≤-m恒成立,
令f(x)=2x+log2x,则f(x)在[1,2]上为增函数,
∴$f(x)_{max}=f(2)={2}^{2}+lo{g}_{2}2=5$,
∴-m≥5,则m≤-5.
∴实数m的取值范围是(-∞,-5].
故答案为:(-∞,-5].
点评 本题考查恒成立问题,考查了函数单调性的性质,体现了分离变量法,是中档题.

练习册系列答案
相关题目
17.已知α是锐角,$\overrightarrow a=({\frac{3}{4},sinα}),\overrightarrow b=({cosα,\frac{1}{{\sqrt{3}}}})$,且$\overrightarrow a$∥$\overrightarrow b$,则α为( )
| A. | 15o | B. | 30o | C. | 30o或60o | D. | 15o或75o |
2.已知A={x|x2-2x-3≤0},B={x|x=2n-1,n∈N*},则A∩B=( )
| A. | {1,3} | B. | {-1,1,3} | C. | {-1,1} | D. | {0,2} |
12.一个口袋内装有大小相同的红、蓝球各一个,若有放回地摸出一个球并记下颜色为一次试验,试验共进行三次,则至少摸到一次红球的概率是( )
| A. | $\frac{1}{8}$ | B. | $\frac{7}{8}$ | C. | $\frac{3}{8}$ | D. | $\frac{5}{8}$ |
19.某算法的程序框图如图所示,若输x的值为2,则输出y的值是( )
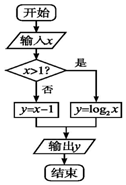

| A. | 1 | B. | 2 | C. | 4 | D. | 以上都不对 |
17.平面内给定三个向量$\overrightarrow{a}$=(3,2),$\overrightarrow{b}$=(-1,2),$\overrightarrow{c}$=(4,1),若($\overrightarrow{a}$+k$\overrightarrow{c}$)∥(2$\overrightarrow{b}$-$\overrightarrow{a}$)则实数k的值为( )
| A. | $\frac{16}{13}$ | B. | $\frac{3}{4}$ | C. | $-\frac{16}{13}$ | D. | $-\frac{4}{3}$ |