题目内容
(本题满分12分)已知椭圆 的对称中心为原点
的对称中心为原点 ,焦点在
,焦点在 轴上,左右焦点分别为
轴上,左右焦点分别为 和
和 ,且
,且 ,点
,点 在该椭圆上.
在该椭圆上.
(1)求椭圆 的方程;
的方程;
(2)过 的直线
的直线 与椭圆
与椭圆 相交于
相交于 两点,若
两点,若 的面积为
的面积为 ,求以
,求以 为圆心且与直线
为圆心且与直线 相切圆的方程.
相切圆的方程.
(1)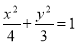 ;(2)
;(2)
【解析】
试题分析:(1)设椭圆的方程,若焦点明确,设椭圆的标准方程,结合条件用待定系数法求出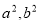 的值,若不明确,需分焦点在
的值,若不明确,需分焦点在 轴和
轴和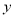 轴上两种情况讨论;(2)解决直线和椭圆的综合问题时注意:第一步:根据题意设直线方程,有的题设条件已知点,而斜率未知;有的题设条件已知斜率,点不定,可由点斜式设直线方程.第二步:联立方程:把所设直线方程与椭圆的方程联立,消去一个元,得到一个一元二次方程.第三步:求解判别式
轴上两种情况讨论;(2)解决直线和椭圆的综合问题时注意:第一步:根据题意设直线方程,有的题设条件已知点,而斜率未知;有的题设条件已知斜率,点不定,可由点斜式设直线方程.第二步:联立方程:把所设直线方程与椭圆的方程联立,消去一个元,得到一个一元二次方程.第三步:求解判别式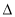 :计算一元二次方程根.第四步:写出根与系数的关系.第五步:根据题设条件求解问题中结论.
:计算一元二次方程根.第四步:写出根与系数的关系.第五步:根据题设条件求解问题中结论.
试题解析:(1)由题知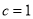 ,
,
椭圆的焦点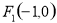 ,
,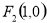
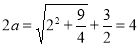
 椭圆C的方程为
椭圆C的方程为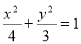 (4分)
(4分)
①当直线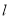 ⊥x轴时,可得A(-1,-
⊥x轴时,可得A(-1,- ),B(-1,
),B(-1, ),
),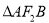 的面积为3,
的面积为3,
不符合题意. (6分)
②当直线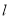 与x轴不垂直时,设直线
与x轴不垂直时,设直线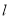 的方程为
的方程为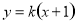 .代入椭圆方程得:
.代入椭圆方程得:
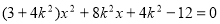 ,显然
,显然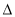 >0成立,设A
>0成立,设A ,B
,B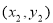 ,则
,则
 ,
, ,可得|AB|=
,可得|AB|= (10分)
(10分)
又圆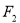 的半径
的半径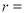
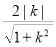 ,∴
,∴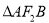 的面积=
的面积=
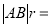
 =
= ,化简得:17
,化简得:17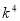 +
+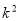 -18=0,得k=±1,∴r =
-18=0,得k=±1,∴r = ,圆的方程为
,圆的方程为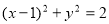 (12分)
(12分)
考点:1、椭圆的标准方程;2、直线与椭圆的综合问题.
考点分析: 考点1:椭圆的标准方程 考点2:椭圆的几何性质 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
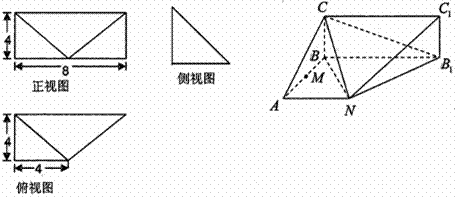
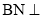 平面
平面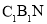 ;
; 为直线
为直线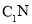 与平面
与平面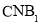 所成的角,求
所成的角,求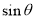 的值;
的值;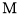 为
为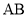 中点,在
中点,在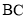 边上求一点
边上求一点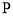 ,使
,使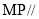 平面
平面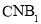 ,求
,求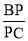 的值.[来源:Zxxk.Co
的值.[来源:Zxxk.Co ,
, ,则
,则
 B.
B. C.
C. D.
D.
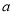 ,
,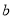 是两条不同的直线,
是两条不同的直线,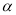 ,
,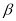 是两个不同的平面,
是两个不同的平面, ,
,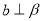 ,则
,则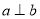 的
的 ,
, ,则
,则
 B.
B. C.
C. D.
D.
 y2 =1,点F1,F2为其两个焦点,点P为双曲线上一点,若P F1⊥P F2,则
y2 =1,点F1,F2为其两个焦点,点P为双曲线上一点,若P F1⊥P F2,则 表示的平面区域为Ω,若在区域Ω内任取一点P(x,y),则点P的坐标满足不等式x2+y2≤2的概率为( )
表示的平面区域为Ω,若在区域Ω内任取一点P(x,y),则点P的坐标满足不等式x2+y2≤2的概率为( )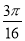 (B)
(B)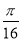 (C)
(C)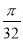 (D)
(D)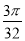
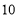 名成员中选
名成员中选 人参加省级数学竞赛,则甲、乙
人参加省级数学竞赛,则甲、乙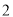 人至少有
人至少有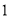 人入选,而丙没有入选的不同选法的种数为 (用数字作答).
人入选,而丙没有入选的不同选法的种数为 (用数字作答).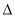 APB面积的最大值为2
APB面积的最大值为2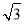 .
.
