题目内容
(本小题满分13分)已知A(-2,0),B(2,0)为椭圆C的左、右顶点,F为其右焦点,P是椭圆C上异于A,B的动点,且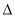 APB面积的最大值为2
APB面积的最大值为2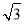 .
.
(1)求椭圆C的方程及离心率;
(2)直线AP与椭圆在点B处的切线交于点D,当直线AP绕点A转动时,试判断以BD为直径的圆与直线PF的位置关系,并加以证明.


(1)椭圆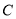 的方程为
的方程为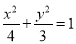 ,离心率为
,离心率为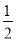 ;(2)以
;(2)以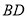 为直径的圆与直线
为直径的圆与直线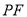 相切.
相切.
【解析】
试题分析:(1)利用待定系数法进行求解;(2)设出直线的方程,联立直线与椭圆的方程,整理成关于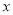 的一元二次方程,利用中点坐标公式求其线段中点,写出圆的方程,利用圆心到直线的距离公式进行证明.
的一元二次方程,利用中点坐标公式求其线段中点,写出圆的方程,利用圆心到直线的距离公式进行证明.
试题解析:(1)由题意可设椭圆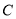 的方程为
的方程为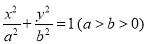 ,
,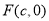 .
.
由题意知
解得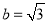 ,
,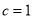 . 3分
. 3分
故椭圆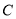 的方程为
的方程为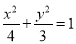 ,离心率为
,离心率为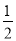 . 5分
. 5分
(Ⅱ)以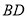 为直径的圆与直线
为直径的圆与直线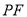 相切.
相切.
证明如下:由题意可设直线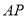 的方程为
的方程为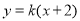
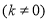 .
.
则点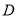 坐标为
坐标为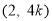 ,
, 中点
中点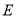 的坐标为
的坐标为 . 6分
. 6分
由 得
得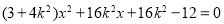 . 7分
. 7分
设点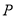 的坐标为
的坐标为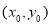 ,则
,则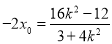 .
.
所以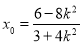 ,
,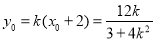 . 9分
. 9分
因为点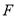 坐标为
坐标为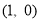 ,
,
当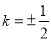 时,点
时,点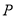 的坐标为
的坐标为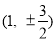 ,点
,点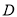 的坐标为
的坐标为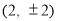 .
.
直线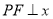 轴,此时以
轴,此时以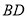 为直径的圆
为直径的圆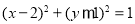 与直线
与直线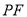 相切. 10分
相切. 10分
当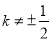 时,则直线
时,则直线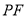 的斜率
的斜率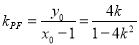 .
.
所以直线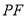 的方程为
的方程为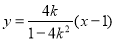 .
.
点 到直线
到直线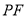 的距离
的距离
 .
.
又因为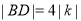 ,所以
,所以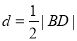 .
.
故以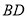 为直径的圆与直线
为直径的圆与直线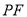 相切.
相切.
综上得,当直线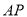 绕点
绕点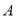 转动时,以
转动时,以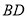 为直径的圆与直线
为直径的圆与直线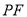 相切.
相切.
考点:1.椭圆的标准方程;2.直线椭圆的位置关系;3.直线与圆的位置关系.
考点分析: 考点1:椭圆的标准方程 考点2:椭圆的几何性质 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
 的对称中心为原点
的对称中心为原点 ,焦点在
,焦点在 轴上,左右焦点分别为
轴上,左右焦点分别为 和
和 ,且
,且 ,点
,点 在该椭圆上.
在该椭圆上. 的方程;
的方程; 的直线
的直线 与椭圆
与椭圆 相交于
相交于 两点,若
两点,若 的面积为
的面积为 ,求以
,求以 为圆心且与直线
为圆心且与直线 的夹角为
的夹角为 ,
, ( )
( ) B.
B. C.
C. D.
D.
 ;②
;②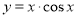 ;③
;③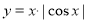 ; ④
; ④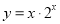 的图象(部分)如下,但顺序被打乱,则按照从左到右将图象对应的函数序号安排正确的一组是
的图象(部分)如下,但顺序被打乱,则按照从左到右将图象对应的函数序号安排正确的一组是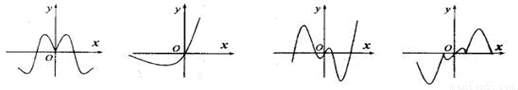
 的模为
的模为 D.
D.
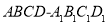 的中心为
的中心为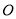 ,面
,面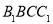 的中心为
的中心为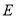 ,
,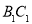 的中点为
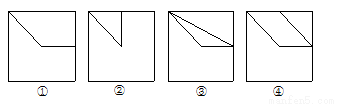
的中点为 则空间四边形
则空间四边形 在该正方体各个面上的投影可能是 .(把你认为正确命题的序号填写在答题纸上)
在该正方体各个面上的投影可能是 .(把你认为正确命题的序号填写在答题纸上)
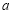 为如图所示的程序框图中输出的结果,则化简
为如图所示的程序框图中输出的结果,则化简 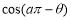 的结果是
的结果是
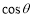 B.
B.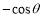 C.
C.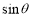 D.
D.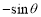
 。
。