题目内容
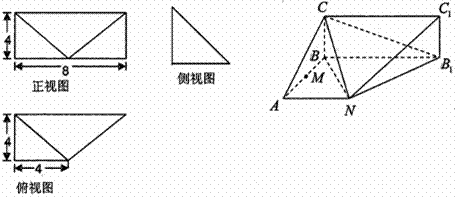
(本小题满分14分)已知某几何体的直观图和三视图如下图所示,其中正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形.
(1)求证: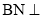 平面
平面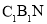 ;
;
(2)设 为直线
为直线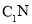 与平面
与平面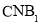 所成的角,求
所成的角,求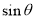 的值;
的值;
(3)设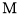 为
为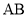 中点,在
中点,在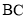 边上求一点
边上求一点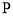 ,使
,使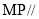 平面
平面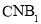 ,求
,求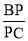 的值.[来源:Zxxk.Co
的值.[来源:Zxxk.Co
(1)(2)  (3)
(3) 
【解析】
试题分析:(1)由三视图可得 两两垂直,则以以
两两垂直,则以以 分别为
分别为 轴建立空间直角坐标系, 可证
轴建立空间直角坐标系, 可证 ,
, ,即
,即
(2)求出平面 的一个法向量
的一个法向量 及
及 ,代入公式
,代入公式 即可求出
即可求出 的值
的值
(3)设 为
为 上一点, 则
上一点, 则 ,
,  ,由
,由 可得
可得 即当
即当 时
时

试题解析:(1)证明∵该几何体的正视图为矩形,侧视图为等腰直角三角形,
俯视图为直角梯形,∴ 两两垂直.
两两垂直.
且 ,
,
以 分别为
分别为 轴建立空间直角坐标系,如图
轴建立空间直角坐标系,如图
则
∵

∴ 且
且 ,
,
∴ )
)
(2)设 为平面
为平面 的一个法向量,
的一个法向量,
则

则
(3) 设
设 为
为 上一点,
上一点,
则 ,
,  1,
1,
∴ 
又 ,
,
∴当 时
时

考点:利用空间向量研究立体几何有关问题
考点分析: 考点1:点、线、面之间的位置关系 考点2:三视图和直观图 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
 ,若
,若 ,则实数
,则实数 的值为( )
的值为( ) B.
B. C.
C. D.
D.
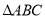 中“
中“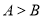 ”是“
”是“ ”的( )
”的( )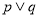 为真命题,则
为真命题,则 为真命题
为真命题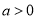 ,
,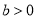 ”是“
”是“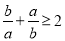 ”的充分必要条件
”的充分必要条件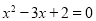 ,则
,则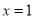 或
或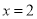 ”的逆否命题为“若
”的逆否命题为“若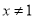 或
或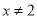 ,则
,则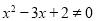 ”
”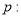
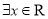 ,使得
,使得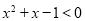 ,则
,则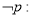
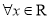 ,使得
,使得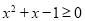
 中,
中, ,
, ,
, ,则( )
,则( ) 或
或 B.
B. C.
C. D.以上答案都不对
D.以上答案都不对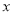 ,
, 满足
满足 ,若目标函数
,若目标函数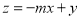 的最大值为
的最大值为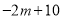 ,最小值为
,最小值为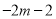 ,则实数
,则实数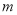 的取值范围是 .
的取值范围是 .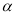 ,
,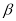 ,
,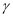 为平面,
为平面,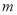 ,
,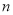 为直线,则
为直线,则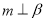 的一个充分条件是( )
的一个充分条件是( )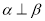 ,
,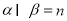 ,
,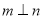 B.
B.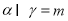 ,
, ,
,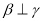
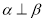 ,
,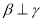 ,
,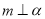 D.
D.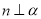 ,
,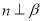 ,
,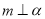
 ,
, ,则
,则 .
. 的对称中心为原点
的对称中心为原点 ,焦点在
,焦点在 轴上,左右焦点分别为
轴上,左右焦点分别为 和
和 ,且
,且 ,点
,点 在该椭圆上.
在该椭圆上. 的方程;
的方程; 的直线
的直线 与椭圆
与椭圆 相交于
相交于 两点,若
两点,若 的面积为
的面积为 ,求以
,求以 为圆心且与直线
为圆心且与直线