Question

【题目】设直线分别是函数 图象上点处的切线，垂直相交于点，且分别与轴相交于点A，B，则△PAB的面积的取值范围是( )

A. (1,+∞) B. (0,2) C. (0,+∞) D. (0,1)

Answer 1

【答案】D

【解析】

设出点P1，P2的坐标，求出原分段函数的导函数，得到直线l1与l2的斜率，由两直线垂直求得P1，P2的横坐标的乘积为1，再分别写出两直线的点斜式方程，求得A，B两点的纵坐标，得到|AB|，联立两直线方程求得P的横坐标，然后代入三角形面积公式，利用基本不等式求得△PAB的面积的取值范围．

解：设P1（x1，y1），P2（x2，y2）（0＜x1＜1＜x2），

当0＜x＜1时，f′（x），当x＞1时，f′（x），

∴l1的斜率，l2的斜率，

∵l1与l2垂直，且x2＞x1＞0，

∴，即x1x2＝1．

直线l1：，l2：．

取x＝0分别得到A（0，1﹣lnx1），B（0，﹣1+lnx2），

|AB|＝|1﹣lnx1﹣（﹣1+lnx2）|＝|2﹣（lnx1+lnx2）|＝|2﹣lnx1x2|＝2．

联立两直线方程可得交点P的横坐标为x，

∴|AB||xP|．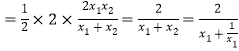

∵函数y＝x在（0，1）上为减函数，且0＜x1＜1，

∴，则，

∴．

∴△PAB的面积的取值范围是（0，1）．

故选：D．