题目内容
【题目】某商店经营的某种消费品的进价为每件14元,月销售量![]() (百件)与每件的销售价格
(百件)与每件的销售价格![]() (元)的关系如图所示,每月各种开支2 000元.
(元)的关系如图所示,每月各种开支2 000元.

(1)写出月销售量![]() (百件)关于每件的销售价格
(百件)关于每件的销售价格![]() (元)的函数关系式.
(元)的函数关系式.
(2)写出月利润![]() (元)与每件的销售价格
(元)与每件的销售价格![]() (元)的函数关系式.
(元)的函数关系式.
(3)当该消费品每件的销售价格为多少元时,月利润最大?并求出最大月利润.
【答案】(1) 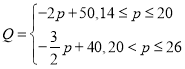 ;(2)
;(2) 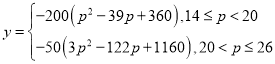 ;(3) 当该消费品每件的销售价格为学
;(3) 当该消费品每件的销售价格为学![]() 时,月利润最大,为4050元
时,月利润最大,为4050元
【解析】
(1)根据函数的图象为分段函数,分别求得当![]() 和
和![]() 时,求得函数的解析式,即可得到答案;
时,求得函数的解析式,即可得到答案;
(2)由(1)中的函数,结合题意,即可求得月利润![]() (元)与每件的销售价格
(元)与每件的销售价格![]() (元)的函数关系式.
(元)的函数关系式.
(3)由(2)中的解析式,结合二次函数的性质,分别求得当![]() 和
和![]() 的最大值,即可求解.
的最大值,即可求解.
(1)由题意,当![]() 时,设函数
时,设函数![]() ,
,
由![]() ,解得
,解得![]() ,所以
,所以![]() ,
,
同理可得当![]() 时,
时,![]() ,
,
所以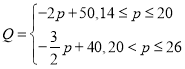 .
.
(2)当![]() 时,
时,![]() ,
,
即![]() ;
;
当![]() 时,
时,![]() ,
,
即![]() ,
,
所以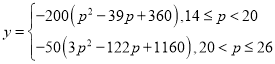 .
.
(3)由(2)中的解析式和二次函数的知识,可得
当![]() 时,则
时,则![]() 时,
时,![]() 取到最大值,为4050;
取到最大值,为4050;
当![]() 时,则
时,则![]() 时,
时,![]() 取到最大值,为
取到最大值,为![]() .
.
又由![]() ,所以当该消费品每件的销售价格为学
,所以当该消费品每件的销售价格为学![]() 时,月利润最大,为4050元.
时,月利润最大,为4050元.

【题目】峰谷电是目前在城市居民当中开展的一种电价类别.它是将一天24小时划分成两个时间段,把8:00—22:00共14小时称为峰段,执行峰电价,即电价上调;22:00—次日8:00共10个小时称为谷段,执行谷电价,即电价下调.为了进一步了解民众对峰谷电价的使用情况,从某市一小区随机抽取了50 户住户进行夏季用电情况调查,各户月平均用电量以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:度)分组的频率分布直方图如下图:
(单位:度)分组的频率分布直方图如下图:

若将小区月平均用电量不低于700度的住户称为“大用户”,月平均用电量低于700度的住户称为“一般用户”.其中,使用峰谷电价的户数如下表:
月平均用电量(度) |
|
|
|
|
|
|
使用峰谷电价的户数 | 3 | 9 | 13 | 7 | 2 | 1 |
(1)估计所抽取的 50户的月均用电量的众数和平均数(同一组中的数据用该组区间的中点值作代表);
(2)(![]() )将“一般用户”和“大用户”的户数填入下面
)将“一般用户”和“大用户”的户数填入下面![]() 的列联表:
的列联表:
一般用户 | 大用户 | |
使用峰谷电价的用户 | ||
不使用峰谷电价的用户 |
(![]() )根据(
)根据(![]() )中的列联表,能否有
)中的列联表,能否有![]() 的把握认为 “用电量的高低”与“使用峰谷电价”有关?
的把握认为 “用电量的高低”与“使用峰谷电价”有关?
| 0.025 | 0.010 | 0.001 |
| 5.024 | 6.635 | 10.828 |
附:![]() ,
,
