题目内容
【题目】已知点![]() 在椭圆
在椭圆![]() 上,
上, ![]() 为椭圆
为椭圆![]() 的右焦点,
的右焦点, ![]() 分别为椭圆
分别为椭圆![]() 的左,右两个顶点.若过点
的左,右两个顶点.若过点![]() 且斜率不为0的直线
且斜率不为0的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且线段
两点,且线段![]() 的斜率之积为
的斜率之积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() 与
与![]() 相交于点
相交于点![]() ,证明:
,证明: ![]() 三点共线.
三点共线.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】试题分析:
(1)根据点![]() 在椭圆上和
在椭圆上和![]() 的斜率之积为
的斜率之积为![]() 可得到关于
可得到关于![]() 的方程组,解方程组后可得椭圆的方程.(2)由(1)可得
的方程组,解方程组后可得椭圆的方程.(2)由(1)可得![]() 轴,要证
轴,要证![]() 三点共线,只需证
三点共线,只需证![]() 轴,即证
轴,即证![]() ,即证直线
,即证直线![]() 与
与![]() 交点的横坐标为1.根据题意可得直线
交点的横坐标为1.根据题意可得直线![]() ,
, ![]() ,故只需证当x=1时,
,故只需证当x=1时, ![]() 成立即可,结合由直线
成立即可,结合由直线![]() 的方程和椭圆方程联立消元后得到的二次方程可得
的方程和椭圆方程联立消元后得到的二次方程可得![]() 显然成立,故得所证结论成立.
显然成立,故得所证结论成立.
试题解析:
(1)∵点![]() 在椭圆
在椭圆![]() ,
,
∴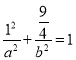 ①.
①.
设![]() ,由线段
,由线段![]() 的斜率之积为
的斜率之积为![]() 得,
得,
![]()
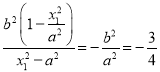 ,
,
∴![]() ②,
②,
由①②解得, ![]() ,
, ![]() .
.
所以椭圆![]() 的方程为
的方程为![]() .
.
(2)由(1)可得![]() 轴,要证
轴,要证![]() 三点共线,只需证
三点共线,只需证![]() 轴,即证
轴,即证![]() .
.
由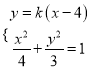 消去y整理得
消去y整理得![]() ,
,
∵直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,
两点,
∴![]()
设![]() ,
, ![]() ,
,
则![]() ,
, ![]() (*),
(*),
因为直线![]() ,
, ![]() ,
,
即证: ![]() ,
,
即证![]()
![]() .
.
即证![]() .
.
将(*)代入上式可得![]() ,
,
整理得![]() .
.
此式明显成立,故原命题得证.
所以![]() 三点共线.
三点共线.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目