题目内容
1.已知数列{an}是等差数列,若$\frac{{{a_{12}}}}{{{a_{11}}}}<-1$,且它的前n项和sn有最大值,则使得sn>0的n的最大值为( )| A. | 11 | B. | 12 | C. | 21 | D. | 22 |
分析 由$\frac{{{a_{12}}}}{{{a_{11}}}}<-1$,它们的前n项和Sn有最大可得a11>0,a11+a12<0,a12<0,从而有a1+a21=2a11>0,a1+a22=a11+a12<0,从而可求满足条件的n的值.
解答 解:由$\frac{{{a_{12}}}}{{{a_{11}}}}<-1$,它们的前n项和Sn有最大值,可得数列的d<0,
∴a11>0,a11+a12<0,a12<0,
∴a1+a21=2a11>0,a1+a22=a11+a12<0,
使得Sn>0的n的最大值n=21,
故选:C.
点评 本题主要考查了等差数列的性质在求解和的最值中应用,解题的关键是灵活利用和公式及等差数列的性质.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
11.在平行四边形ABCD中,AB=3,AD=4,则$\overrightarrow{AC}$•($\overrightarrow{AB}$-$\overrightarrow{AD}$)等于( )
| A. | -7 | B. | 1 | C. | 7 | D. | 25 |
16.一个几何体的三视图如图所示,则该几何体的体积是( )
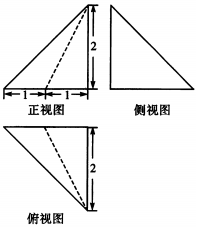

| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{8}{3}$ |
6.已知点P是△ABC所在平面内一点,且$\overrightarrow{PA}$=-2$\overrightarrow{PB}$,在△ABC内任取一点Q,则Q落在△APC内的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
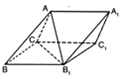 如图,三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,AC=AB1.
如图,三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,AC=AB1.