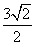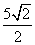题目内容
如图,四棱锥PABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.
(1) 证明:PA⊥BD;
(2) 若PD=AD,求二面角APBC的余弦值.
(1)证明:因为∠DAB=60°,AB=2AD,由余弦定理得BD=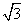 AD.
AD.
从而BD2+AD2=AB2,故BD⊥AD.
又PD⊥底面ABCD,可得BD⊥PD.又AD∩PD=D.所以BD⊥平面PAD.故PA⊥BD.
(2) 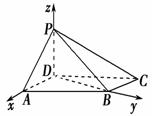 解:如图,以D为坐标原点,AD的长为单位长,射线
解:如图,以D为坐标原点,AD的长为单位长,射线
DA为x轴的正半轴建立空间直角坐标系Dxyz,则
A(1,0,0),B(0,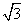 ,0),C(-1,
,0),C(-1,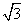 ,0),P(0,0,1).
,0),P(0,0,1).
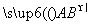 =(-1,
=(-1,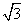 ,0),
,0),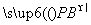 =(0,
=(0,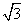 ,-1),
,-1),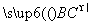 =(-1,0,0).
=(-1,0,0).
设平面PAB的法向量为n=(x,y,z),
则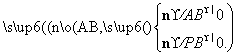 即
即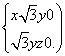 因此可取n=(
因此可取n=(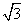 ,1,
,1,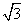 ).
).
设平面PBC的法向量为m,则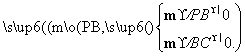 可取m=(0,-1,-
可取m=(0,-1,-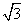 ),
),
则cos〈m,n〉=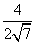 =-
=-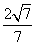 .故二面角APBC的余弦值为-
.故二面角APBC的余弦值为-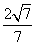 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,
中, 是斜边
是斜边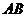 上的高,则下列等式中不成立的是 ( ).
上的高,则下列等式中不成立的是 ( ). B.
B.
 D.
D.
 ,当
,当 变化时所得的直线都经过的定点为____________.
变化时所得的直线都经过的定点为____________. 且与
且与 有相同焦点的椭圆的方程是
有相同焦点的椭圆的方程是 B.
B. C.
C. D.
D.
 、
、 两两的夹角均为60°,且|
两两的夹角均为60°,且| |等于______.
|等于______. ,且
,且 ,则实数
,则实数 的值为( )
的值为( )



 ,则
,则 ________.
________.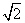 围成的三角形区域(包含边界)为D,P(x,y)为D内的一个动点,则目标函数z=
围成的三角形区域(包含边界)为D,P(x,y)为D内的一个动点,则目标函数z=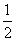 x-y的最小值为( )
x-y的最小值为( )