题目内容
已知tan(α-β)=
解:∵tanα=tan[(α-β)+β]=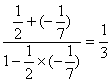 ,
,
∴tan2α=![]() .
.
∵tanα=![]() >0且α∈(0,π),可推得α∈(0,
>0且α∈(0,π),可推得α∈(0,![]() ).
).
又tan2α=![]() >0,可推得2α∈(0,
>0,可推得2α∈(0,![]() ),
),
同理,得β∈(![]() ,π).
,π).
∴2α-β∈(-π,0).
又tan(2α-β)= =1,∴2α-β=
=1,∴2α-β=![]() π.
π.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知tan(θ+
)=-3,则sin2θ+sinθcosθ-2cos2θ=( )
| π |
| 4 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|