题目内容
19．已知p：M={（x，y）|tx-y≤3}，且（2，1）∈M，（1，-4）∉M，q：集合A={x|-2≤x≤5}，B={x|t+1≤x≤2t-1}，且B⊆A，若p或q为真，p且q为假，求t的取值范围．分析 分别求出命题为真，为假时，t的取值范围，根据复合命题的真假判断所有可能的组合，最后求出t的范围．
解答 解：若命题p为真命题，则$\left\{\begin{array}{l}{2t-1≤3}\\{t+4＞3}\end{array}\right.$，解得-1＜t≤2．
∴若命题p为假命题，则t≤-1或t＞2．
若命题q是真命题，则t+1＞2t-1或$\left\{\begin{array}{l}{t+1≥-2}\\{2t-1≤5}\\{t+1≤2t-1}\end{array}\right.$，解得t≤3，
∴若命题q为假命题，则t＞3．
∵p或q为真，p且q为假，∴p为真，q为假或p为假，q为真．
∴t的范围是[（-1，2]∩（3，+∞）]∪{[（-∞，-1]∪（2，+∞）]∩（-∞，3]}=（-∞，-1]∪（2，3]．
点评 本题考查了复合命题的真假判断，集合运算，属于中档题．
练习册系列答案
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
9．将函数y=f（x）的图象沿x轴向左平移π个单位后，再将所得图象上各点的横坐标缩小为原来的一半，得到函数y=sinx的图象，那么y=f（x）的表达式为（ ）
| A． | y=sin2x | B． | y=-sin2x | C． | $y=-cos\frac{x}{2}$ | D． | $y=-sin\frac{x}{2}$ |
7．
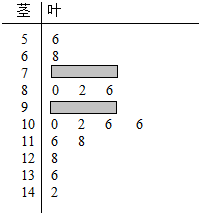某数学老师对本校2013届高三学生的高考数学成绩按1：200进行分层抽样抽取了20名学生的成绩，并用茎叶图记录分数如图所示，但部分数据不小心丢失，同时得到如下所示的频率分布表：
（1）求表中a，b的值
（2）求分数在[90，100）范围内的学生人数，并估计这次考试全校学生数学成绩的及格率（分数在[90，150）内为及格）；
（3）从成绩在[100，130）范围内的学生中随机选4人，求其中成绩在[100，110）内的人数最多2人的概率．
某数学老师对本校2013届高三学生的高考数学成绩按1：200进行分层抽样抽取了20名学生的成绩，并用茎叶图记录分数如图所示，但部分数据不小心丢失，同时得到如下所示的频率分布表：| 分数段（分） | [50，70） | [70，90） | [90，110） | [110，130） | [130，150） | 总计 |
| 频数 | b | |||||
| 频率 | a | 0.25 |
（2）求分数在[90，100）范围内的学生人数，并估计这次考试全校学生数学成绩的及格率（分数在[90，150）内为及格）；
（3）从成绩在[100，130）范围内的学生中随机选4人，求其中成绩在[100，110）内的人数最多2人的概率．
4．下列式子中表示正确的是（ ）
| A． | 2+cosx=4 | B． | $\sqrt{10}$＞π | C． | sinx•cosx=sin2x | D． | sin75°＞cos14° |