题目内容
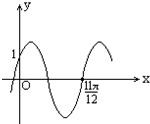
已知如图是函数y=2sin(ωx+φ)(|φ|< )的图象,那么( )
)的图象,那么( )
A.?=
 ,φ=
,φ=
B.?=
 ,φ=-
,φ=-
C.?=2,φ=

D.?=2,φ=-

【答案】分析:由图象过(0,1)及|φ|< ,求出ψ的值,函数图象过点(
,求出ψ的值,函数图象过点( ,0),据五点法作图的过程知ω•
,0),据五点法作图的过程知ω• +
+ =2π,求出ω.
=2π,求出ω.
解答:解:因为函数图象过(0,1),所以,1=2sinφ,∴sinφ= ,∵|φ|<
,∵|φ|< ,
,
∴φ= ,故函数y=2sin(ωx+
,故函数y=2sin(ωx+ ),又∵函数图象过点(
),又∵函数图象过点( ,0),
,0),
∴0=2sin(ω• +
+ ),由五点法作图的过程知,ω•
),由五点法作图的过程知,ω• +
+ =2π,
=2π,
∴ω=2,综上,φ= ,ω=2,
,ω=2,
故选C.
点评:本题考查五点法作图的方法,在本题图中的一个完整的标准周期内,图象上的五个关键点的横坐标分别为:0, ,π,
,π, ,2π.
,2π.
 ,求出ψ的值,函数图象过点(
,求出ψ的值,函数图象过点( ,0),据五点法作图的过程知ω•
,0),据五点法作图的过程知ω• +
+ =2π,求出ω.
=2π,求出ω.解答:解:因为函数图象过(0,1),所以,1=2sinφ,∴sinφ=
 ,∵|φ|<
,∵|φ|< ,
,∴φ=
 ,故函数y=2sin(ωx+
,故函数y=2sin(ωx+ ),又∵函数图象过点(
),又∵函数图象过点( ,0),
,0),∴0=2sin(ω•
 +
+ ),由五点法作图的过程知,ω•
),由五点法作图的过程知,ω• +
+ =2π,
=2π,∴ω=2,综上,φ=
 ,ω=2,
,ω=2,故选C.
点评:本题考查五点法作图的方法,在本题图中的一个完整的标准周期内,图象上的五个关键点的横坐标分别为:0,
 ,π,
,π, ,2π.
,2π. 
练习册系列答案
相关题目
已知如图是函数y=2sin(ωx+φ)(|φ|<
)的图象,那么( )
| π |
| 2 |

A、?=
| ||||
B、?=
| ||||
C、?=2,φ=
| ||||
D、?=2,φ=-
|
 已知如图是函数y=2sin(ωx+φ)(|φ|<
已知如图是函数y=2sin(ωx+φ)(|φ|< )图像上的一段,则( )
)图像上的一段,则( ) ,φ=
,φ= (B)ω=
(B)ω=
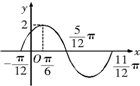
 )的图象上的一段,则( )
)的图象上的一段,则( )
 ,φ=
,φ=
 ,φ=-
,φ=-

