题目内容
对于函数f(x)=2sinxcosx,下列选项中正确的是
- A.f(x)在
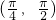 上递增
上递增 - B.f(x)的最大值为2
- C.f(x)的图象关于点
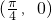 对称
对称 - D.f(x)的图象关于直线
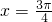 对称
对称
D
分析:首先将函数解析式化简为f(x)=sin2x,再结合正弦函数的单调性、最值和图象对称性的公式,对各个选项加以判断,即可得到正确答案.
解答:根据二倍角正弦公式,得f(x)=2sinxcosx=sin2x,
对于A,当x∈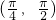 时,2x∈
时,2x∈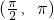 ,可得此时f(x)=sin2x是减函数,故A不正确;
,可得此时f(x)=sin2x是减函数,故A不正确;
对于B,f(x)=sin2x的最大值是1,故B错;
对于C,因为f( )=sin
)=sin =1为函数的最大值,故直线x=
=1为函数的最大值,故直线x= 是函数图象的一条对称轴,
是函数图象的一条对称轴,
但f(x)的图象不关于点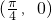 对称,故C不正确;
对称,故C不正确;
对于D,因为f( )=sin(
)=sin( )=-1为函数的最小值,
)=-1为函数的最小值,
故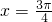 是函数图象的一条对称轴,故D正确.
是函数图象的一条对称轴,故D正确.
故选D
点评:本题以函数y=sin2x为例,考查了正弦函数的单调性与奇偶性,值域与最值和图象的对称性等知识,属于基础题.
分析:首先将函数解析式化简为f(x)=sin2x,再结合正弦函数的单调性、最值和图象对称性的公式,对各个选项加以判断,即可得到正确答案.
解答:根据二倍角正弦公式,得f(x)=2sinxcosx=sin2x,
对于A,当x∈
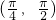 时,2x∈
时,2x∈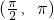 ,可得此时f(x)=sin2x是减函数,故A不正确;
,可得此时f(x)=sin2x是减函数,故A不正确;对于B,f(x)=sin2x的最大值是1,故B错;
对于C,因为f(
 )=sin
)=sin =1为函数的最大值,故直线x=
=1为函数的最大值,故直线x= 是函数图象的一条对称轴,
是函数图象的一条对称轴,但f(x)的图象不关于点
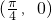 对称,故C不正确;
对称,故C不正确;对于D,因为f(
 )=sin(
)=sin( )=-1为函数的最小值,
)=-1为函数的最小值,故
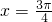 是函数图象的一条对称轴,故D正确.
是函数图象的一条对称轴,故D正确.故选D
点评:本题以函数y=sin2x为例,考查了正弦函数的单调性与奇偶性,值域与最值和图象的对称性等知识,属于基础题.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目