题目内容
12.已知双曲线$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{4}$=1的左焦点为F,点P为双曲线右支上的一点,且PF与圆x2+y2=9相切于点N,M为线段PF的中点,O 为坐标原点,则|MN|-|MO|=1.分析 利用中位线定理可知丨OM丨=$\frac{1}{2}$丨PF1丨,根据勾股定理求得丨MN丨=丨MF丨-丨NF丨=丨MF丨-2,丨MF丨=$\frac{1}{2}$丨PF丨,则利用双曲线的定义,即可求出|MN|-|MO|.
解答 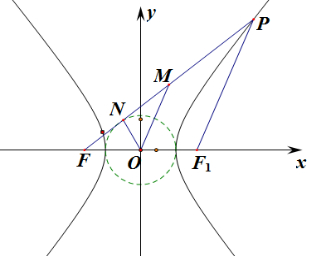 解:由题意可知:双曲线$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{4}$=1焦点在x轴上,a=3,b=2,c=$\sqrt{13}$,
解:由题意可知:双曲线$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{4}$=1焦点在x轴上,a=3,b=2,c=$\sqrt{13}$,
设双曲线的右焦点F1($\sqrt{13}$,0),左焦点F(-$\sqrt{13}$,0),
由OM为△PFF1中位线,则丨OM丨=$\frac{1}{2}$丨PF1丨,
由PF与圆x2+y2=9相切于点N,则△ONF为直角三角形,
∴丨NF丨2=丨OF丨2-丨ON丨2=13-9=4,
则丨NF丨=2,
∴丨MN丨=丨MF丨-丨NF丨=丨MF丨-2,
由丨MF丨=$\frac{1}{2}$丨PF丨,
∴|MN|-|MO|=$\frac{1}{2}$丨PF丨-2-$\frac{1}{2}$丨PF1丨=$\frac{1}{2}$(丨PF丨-丨PF1丨)-2=$\frac{1}{2}$×2a-2=1,
∴|MN|-|MO|=1,
故答案为:1.
点评 本题考查双曲线的定义,考查勾股定理,中位线定理的应用,考查计算能力,属于中档题.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
12.已知函数f(x)=lnx-x2与g(x)=(x-2)2-$\frac{1}{2x-4}$-m的图象上存在关于(1,0)对称的点,则实数m的取值范围是( )
| A. | (-∞,1-ln2) | B. | (-∞,1-ln2] | C. | (1-ln2,+∞) | D. | [1-ln2,+∞) |
4.如图是一个正方体被切掉部分后所得几何体的三视图,则该几何体的体积为( )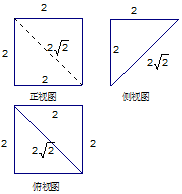

| A. | $\frac{8}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{8\sqrt{2}}{3}$ | D. | $\frac{4\sqrt{2}}{3}$ |
1.设双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点分别为F1,F2,若在曲线C的右支上存在点P,使得△PF1F2的内切圆半径为a,圆心记为M,又△PF1F2的重心为G,满足MG∥F1F2,则双曲线C的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
2.若0<x1<x2<1,则( )
| A. | ex2-ex1>lnx2-lnx1 | B. | ex2-ex1<lnx2-lnx1 | ||
| C. | x2ex1>x1ex2 | D. | x2ex1<x1ex2 |