题目内容
1.在长为10cm的线段AB上任取一点C.现作一矩形,邻边长分别等于线段AC,CB的长,则该矩形面积不小于9cm2的概率为$\frac{4}{5}$.分析 根据几何概型的概率公式,设AC=x,则BC=10-x,由矩形的面积S=x(10-x)≥9可求x的范围,利用几何概率的求解公式可求.
解答 解:设AC=x,则BC=10-x,
矩形的面积S=x(10-x)≥9,
∴x2-10x+9≤0,
∴1≤x≤9,
由几何概率的求解公式可得,矩形面积不小于9cm2的概率P=$\frac{8}{10}=\frac{4}{5}$,
故答案为:$\frac{4}{5}$.
点评 本题主要考查了二次不等式的解法,与区间长度有关的几何概率的求解公式的应用.

练习册系列答案
相关题目
16.如图,在△OAB中,点P在边AB上,且AP:PB=3:2.则$\overrightarrow{OP}$=( )


| A. | $\frac{3}{5}\overrightarrow{OA}+\frac{2}{5}\overrightarrow{OB}$ | B. | $\frac{2}{5}\overrightarrow{OA}+\frac{3}{5}\overrightarrow{OB}$ | C. | $\frac{3}{5}\overrightarrow{OA}-\frac{2}{5}\overrightarrow{OB}$ | D. | $\frac{2}{5}\overrightarrow{OA}-\frac{3}{5}\overrightarrow{OB}$ |
6.已知i是虚数单位,则复数i(1+i)的共轭复数为( )
| A. | 1+i | B. | l-i | C. | -l+i | D. | -l-i |
13.正方体ABCD-A1B1C1D1的棱长为a,E,F分别是BB1,CD的中点,则点F到平面A1D1E的距离为( )
| A. | $\frac{3}{10}$a | B. | $\frac{3\sqrt{7}}{10}$a | C. | $\frac{3\sqrt{5}}{10}$a | D. | $\frac{7}{10}$a |
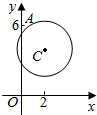 已知某市野生动物园中有猛虎出没,三位青年为抄近路返回市区(从A点出发,沿y轴负方向走直线),决定冒险穿越野生动物园,如图,设老虎出没的区域为圆C:(x-2)2+(y-4)2=$\frac{25}{4}$所含区域,三位青年从A(0,6)到O需要40min,若三位青年在老虎出没的地区逗留时间超过15min就有生命危险.问:三位青年是否有生命危险?(假设三位青年以匀速返回市区)
已知某市野生动物园中有猛虎出没,三位青年为抄近路返回市区(从A点出发,沿y轴负方向走直线),决定冒险穿越野生动物园,如图,设老虎出没的区域为圆C:(x-2)2+(y-4)2=$\frac{25}{4}$所含区域,三位青年从A(0,6)到O需要40min,若三位青年在老虎出没的地区逗留时间超过15min就有生命危险.问:三位青年是否有生命危险?(假设三位青年以匀速返回市区)