题目内容
已知集合S={x|x2-px+q=0}，T={x|x2-（p+3）x+6=0}，且S∩T={3}，则log9（3p+q）= ．
考点：交集及其运算
专题：集合
分析：根据S与T的交集得到x=3为S与T中方程的解，把x=3分别代入求出p与q的值，即可确定出原式的值．
解答：
解：∵S={x|x2-px+q=0}，T={x|x2-（p+3）x+6=0}，且S∩T={3}，
∴3为S与T中方程的解，
把x=3代入S中方程得：9-3p+q=0，
把x=3代入T中方程得：9-3（p+3）+6=0，
解得：p=2，q=-3，
则log9（3p+q）=log93=
．
故答案为：
∴3为S与T中方程的解，
把x=3代入S中方程得：9-3p+q=0，
把x=3代入T中方程得：9-3（p+3）+6=0，
解得：p=2，q=-3，
则log9（3p+q）=log93=
| 1 |
| 2 |
故答案为：
| 1 |
| 2 |
点评：此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
相关题目
设
=（sinx，1），
=（
，cosx），且
∥
，则锐角x为（ ）
| a |
| b |
| 1 |
| 2 |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
设f（x）是定义在R上奇函数，且当x＜0时，f（x）=2x-3，则f（2）等于（ ）
| A、-1 | ||
B、
| ||
| C、1 | ||
D、-
|
函数f(x)=2-x2+2x的值域是（ ）
| A、（-∞，2） |
| B、（-∞，2] |
| C、（0，2） |
| D、（0，2] |
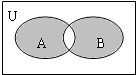设全集U={x|x＜9，且x∈Z}，A={1，2，3}，B={3，4，5，6}，图中阴影部分所表示的集合为（ ）| A、{1，2，3，4，5，6，7，8} |
| B、{1，2，4，5，6} |
| C、{1，2，4，5，6，7，8} |
| D、{1，2，3，4，5，6} |
已知集合A={x|-1≤x≤3}，集合B={x|
＜0}，则A∩B=（ ）
| 1 |
| x |
| A、{x|-1＜x＜0} |
| B、{x|-1≤x＜0} |
| C、{x|x＜0} |
| D、{x|x≤3} |
下列哪组中的函数相等（ ）
A、y=x，y=（
| ||||||
B、y=
| ||||||
C、y=x2，y=
| ||||||
D、y=
|