题目内容

圆ρ= $数学公式$ （cosθ+sinθ）的圆心的极坐标是

A.
（1， $数学公式$ ）
B.
（ $数学公式$ ， $数学公式$ ）
C.
（ $数学公式$ ， $数学公式$ ）
D.
（2， $数学公式$ ）

A
分析：先在极坐标方程ρ= $\text{[math]}$ （cosθ+sinθ）的两边同乘以ρ，再利用直角坐标与极坐标间的关系，即利用ρcosθ=x，ρsinθ=y，ρ²=x²+y²，进行代换化成直角坐标方程求解即得．
解答：将方程ρ= $\text{[math]}$ （cosθ+sinθ）两边都乘以ρ得：ρ²= $\text{[math]}$ pcosθ+ $\text{[math]}$ ρsinθ，
化成直角坐标方程为x²+y²- $\text{[math]}$ x- $\text{[math]}$ y=0．圆心的坐标为（ $\text{[math]}$ ， $\text{[math]}$ ）．
化成极坐标为（1， $\text{[math]}$ ）．
故选A．
点评：本题考查点的极坐标和直角坐标的互化，能在极坐标系中用极坐标刻画点的位置，体会在极坐标系和平面直角坐标系中刻画点的位置的区别，能进行极坐标和直角坐标的互化．

练习册系列答案

阳光作业本课时优化设计系列答案

同步练习指导系列答案

实验指导与实验报告系列答案

通城学典周计划系列答案

新编课时精练系列答案

典范阅读系列答案

一路领先课时练同步测评系列答案

同步练习加过关测试系列答案

名师作业导学号系列答案

高效新学案系列答案

相关题目

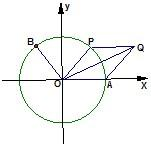如图，A是单位圆与x轴正半轴的交点，点P在单位圆上，∠AOP=θ（0＜θ＜π），

，四边形OAQP的面积为S．
（1）求

+S的最大值及此时θ的值θ₀；
（2）设点B的坐标为(-

)，∠AOB=α，在（1）的条件下求cos（α+θ₀）．

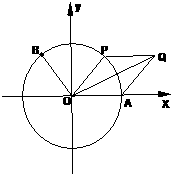（2011•普宁市模拟）如图，A是单位圆与x轴正半轴的交点，点B、P在单位圆上，且B(-

)，∠AOB=α，∠AOP=θ（0＜θ＜π），

，四边形OAQP的面积为S．
（Ⅰ）求cosα+sinα；
（Ⅱ）求

+S的最大值及此时θ的值θ₀．

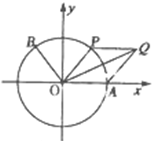（2012•茂名二模）如图，A是单位圆与x轴正半轴的交点，点B，P在单位圆上，且B（-

），∠AOB=α，∠AOP=θ（0＜θ＜π），

．设四边形OAQP的面积为S，
（1）求cos（α-

）；
（2）求f（θ）=

+S的单调递增区间．

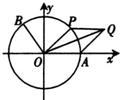（2013•泸州一模）如图，A是单位圆与x轴正半轴的交点，点B、P在单位圆上，且B(-

)，∠AOB=α．
（Ⅰ）求

的值；
（Ⅱ）设平行四边形OAQP的面积为S，∠AOP=θ（0＜θ＜π），f（θ）=（cosθ+S）S，求f（θ）的最大值及此时θ的值．

如图，A是单位圆与x轴正半轴的交点，点B、P在单位圆上，且

．
（Ⅰ）求

的值；
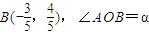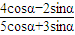（Ⅱ）设平行四边形OAQP的面积为S，∠AOP=θ（0＜θ＜π），f（θ）=（cosθ+S）S，求f（θ）的最大值及此时θ的值．