题目内容
△ABC的内角A，B，C所对的边分别为a，b，c.
(1)若a，b，c成等差数列，证明：sin A＋sin C＝2sin(A＋C)；
(2)若a，b，c成等比数列，求cos B的最小值．
解：(1)∵a，b，c成等差数列，∴a＋c＝2b.
由正弦定理得sin A＋sin C＝2sin B.
∵sin B＝sin[π－(A＋C)]＝sin(A＋C)，
∴sin A＋sin C＝2sin(A＋C)．
(2)∵a，b，c成等比数列，∴b2＝ac.
由余弦定理得
当且仅当a＝c时等号成立，
∴cos B的最小值为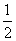
.
练习册系列答案
一线名师提优试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
是自然对数的底数，
.
的单调区间，最大值；
根
的个数.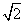
cos 3x的图像( )
个单位 B．向左平移
个单位 D．向左平移
(1)求实验室这一天的最大温差．
.
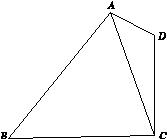
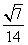，sin∠CBA＝
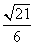，求BC的长．
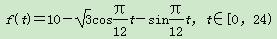(1)求实验室这一天的最大温差．
－sin2x.
的值；
，都有f(x)≤c，求实数c的取值范围．
<
B．a<
，集合
，
，
（ ） 
B．
C．
D．