题目内容
用数学归纳法证明:
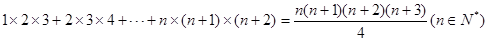 .
.
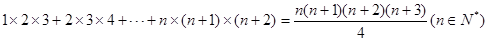 .
.证明:(1)当 时,左边
时,左边 ,右边
,右边 左边,∴等式成立.
左边,∴等式成立.
(2)设当 时,等式成立,
时,等式成立,
即 . 则当
. 则当 时,
时,
左边

∴ 时,等式成立.
时,等式成立.
由(1)、(2)可知,原等式对于任意 成立.
成立.
 时,左边
时,左边 ,右边
,右边 左边,∴等式成立.
左边,∴等式成立.(2)设当
 时,等式成立,
时,等式成立,即
 . 则当
. 则当 时,
时,左边


∴
 时,等式成立.
时,等式成立. 由(1)、(2)可知,原等式对于任意
 成立.
成立.首先证明当n=1时等式成立,再假设n=k时等式成立,得到等式
 ,
,
下面证明当n=k+1时等式左边
 ,
,
根据前面的假设化简即可得到结果,最后得到结论.
 ,
,下面证明当n=k+1时等式左边
 ,
,根据前面的假设化简即可得到结果,最后得到结论.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 (
( )
) 中,
中, 是
是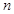 项和,且
项和,且 与
与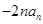 的等差中项,其中
的等差中项,其中 是不等于零的常数.
是不等于零的常数. ; (2)猜想
; (2)猜想 的表达式,并用数学归纳法加以证明.
的表达式,并用数学归纳法加以证明. ,在验证
,在验证 成立时,左边所得的项为 ( )
成立时,左边所得的项为 ( )


 , (a≠1,n∈N)”时,在验证n=1成立时,左边应该是 ( )
, (a≠1,n∈N)”时,在验证n=1成立时,左边应该是 ( )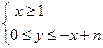 表示的平面区域内可行解的个数,则f(1)=_______;f(2)=_______;f(n)=_______.
表示的平面区域内可行解的个数,则f(1)=_______;f(2)=_______;f(n)=_______. 时,
时, 成立
成立 ,由不等式
,由不等式 ,启发我们归纳得到推广结论:
,启发我们归纳得到推广结论: ,其中
,其中 .
.