题目内容
已知向量a=(sinθ,cosθ),b=(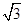 ,1),其中θ∈(0,
,1),其中θ∈(0,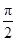 ).
).
(1)若a∥b,求sinθ和cosθ的值;
(2)若f(θ)=(a+b)2,求f(θ)的值域.
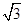 ,1),其中θ∈(0,
,1),其中θ∈(0,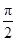 ).
).(1)若a∥b,求sinθ和cosθ的值;
(2)若f(θ)=(a+b)2,求f(θ)的值域.
(1)sinθ= ,cosθ=
,cosθ=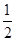 (2)(7,9]
(2)(7,9]
 ,cosθ=
,cosθ=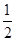 (2)(7,9]
(2)(7,9]解:(1)∵a∥b,
∴sinθ-
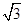 cosθ=0,
cosθ=0,求得tanθ=
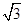 .
.又∵θ∈(0,
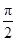 ),
),∴θ=
 ,sinθ=
,sinθ= ,cosθ=
,cosθ=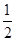 .
.(2)f(θ)=(sinθ+
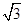 )2+(cosθ+1)2
)2+(cosθ+1)2=2
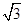 sinθ+2cosθ+5
sinθ+2cosθ+5=4sin(θ+
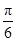 )+5.
)+5.又∵θ∈(0,
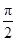 ),
),∴θ+
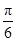 ∈(
∈(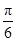 ,
, ),
),∴
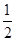 <sin(θ+
<sin(θ+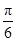 )≤1,
)≤1,∴7<f(θ)≤9,
即函数f(θ)的值域为(7,9].

练习册系列答案
相关题目
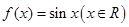 与
与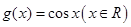 .
.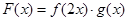 ,有下列结论:①
,有下列结论:①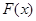 是奇函数;②
是奇函数;②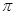 ;③
;③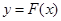 的图象关于点
的图象关于点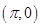 对称;④
对称;④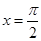 对称.其中正确结论的序号是__________;(直接写出所有正确结论的序号)
对称.其中正确结论的序号是__________;(直接写出所有正确结论的序号)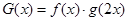 ,求满足
,求满足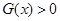 的
的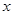 的取值范围;
的取值范围;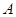 ,函数
,函数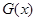 的值域为
的值域为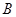 ,试判断集合
,试判断集合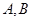 之间的关系.
之间的关系.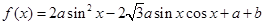 定义域为
定义域为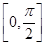 ,值域为[-5,1],求实数
,值域为[-5,1],求实数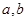 的值。
的值。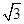 ,sinx),x∈R.
,sinx),x∈R.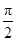 ),证明:a和b不平行;
),证明:a和b不平行; -
- sin2ωx-sinωxcosωx(ω>0),且y=f(x)图象的一个对称中心到最近的对称轴的距离为
sin2ωx-sinωxcosωx(ω>0),且y=f(x)图象的一个对称中心到最近的对称轴的距离为 .
. ]上的最大值和最小值.
]上的最大值和最小值.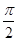 是函数f(x)=cos2
是函数f(x)=cos2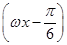 -sin2ωx(ω>0)的两个相邻的零点.
-sin2ωx(ω>0)的两个相邻的零点.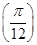 的值;
的值;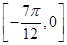 ,都有|f(x)-m|≤1,求实数m的取值范围.
,都有|f(x)-m|≤1,求实数m的取值范围.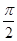 )的部分图象如图所示,则( )
)的部分图象如图所示,则( )

 sinxcosx-cos2x+
sinxcosx-cos2x+ (x∈R),则f(x)在区间
(x∈R),则f(x)在区间 上的值域是________.
上的值域是________. ,下列选项正确的是 ( )
,下列选项正确的是 ( ) 在
在 内是递增的
内是递增的