题目内容
设平面向量a=(cosx,sinx),b=(cosx+2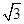 ,sinx),x∈R.
,sinx),x∈R.
(1)若x∈(0,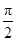 ),证明:a和b不平行;
),证明:a和b不平行;
(2)若c=(0,1),求函数f(x)=a·(b-2c)的最大值,并求出相应的x值.
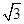 ,sinx),x∈R.
,sinx),x∈R.(1)若x∈(0,
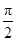 ),证明:a和b不平行;
),证明:a和b不平行;(2)若c=(0,1),求函数f(x)=a·(b-2c)的最大值,并求出相应的x值.
(1)见解析 (2) f(x)max=5,x=2kπ- (k∈Z)
(k∈Z)
 (k∈Z)
(k∈Z)(1)证明:假设a与b平行,
则cosxsinx-sinx(cosx+2
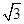 )=0,
)=0,即sinx=0,与x∈(0,
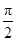 )时,sinx>0,矛盾.
)时,sinx>0,矛盾.故a与b不平行.
(2)解:f(x)=a·b-2a·c
=cos2x+2
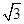 cosx+sin2x-2sinx
cosx+sin2x-2sinx=1-2sinx+2
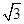 cosx
cosx=1-4sin(x-
 ).
).所以f(x)max=5,x=2kπ-
 (k∈Z).
(k∈Z).
练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
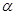 ,使
,使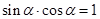
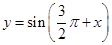 是偶函数
是偶函数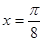 是函数
是函数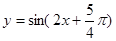 的一条对称轴
的一条对称轴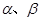 是第一象限的角,且
是第一象限的角,且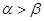 ,则
,则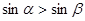
 ,若将函数
,若将函数 的图像向左平移
的图像向左平移 个单位后所得图像与原图像重合,则
个单位后所得图像与原图像重合,则 的值不可能为( )
的值不可能为( ) 在
在 上有两个不同的零点,则实数
上有两个不同的零点,则实数 的取值范围为_________________.
的取值范围为_________________.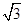 ,1),其中θ∈(0,
,1),其中θ∈(0,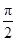 ).
).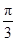 ≤x≤
≤x≤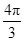 )的最大值与最小值分别为( )
)的最大值与最小值分别为( )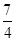 ,最小值为-
,最小值为-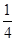
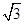 sinωx·cosωx-cos2ωx+λ(x∈R)的图象关于直线x=π对称,其中ω,λ为常数,且ω∈(
sinωx·cosωx-cos2ωx+λ(x∈R)的图象关于直线x=π对称,其中ω,λ为常数,且ω∈(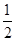 ,1).
,1).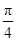 ,0),求函数f(x)的值域.
,0),求函数f(x)的值域.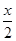 cos
cos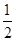
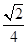 ,α∈(0,π),求α的值;
,α∈(0,π),求α的值;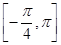 上最大值和最小值.
上最大值和最小值.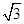 cos x,cos x),b=(sin x,2cos x),设函数f(x)=a·b+|b|2+
cos x,cos x),b=(sin x,2cos x),设函数f(x)=a·b+|b|2+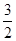 .
.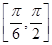 时,求函数f(x)的值域;
时,求函数f(x)的值域;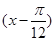 的值;
的值;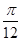 个单位后,再将得到的图象上各点的纵坐标向下平移5个单位,得到函数y=g(x)的图象,求函数g(x)的表达式并判断奇偶性.
个单位后,再将得到的图象上各点的纵坐标向下平移5个单位,得到函数y=g(x)的图象,求函数g(x)的表达式并判断奇偶性.