题目内容

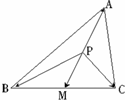（1）△ABC中，P为中线AM上一点，|
AM
|=4，设
AP
=2
PM
，试用
AB
，
AC
表示
PA
；
（2）求
PA
•(
PB
+
PC
)的最小值．
分析：易得M是BC的中点，P是三角形ABC的重心，进而得
PA
•(
PB
+
PC
)=
PA
•2
PM
，由数量积的定义可得答案．
解答：解：（Ⅰ）由于 
PA
=-
AP
=-
2
3
AM
=-
2
3
•
1
2
(
AB
+
AC
)
则
PA
=-
1
3
(
AB
+
AC
)
（Ⅱ）在△PBC中，M为BC的中点，∴
PM
=
1
2
(
PB
+
PC
)
设|
PA
|=x    
则
PA•
(
PA
+
PC
)=2
PA
•
PM
=2|
PA
|•|
PM
|•cosπ=-2x•（4-x）=2x2-8x
当x=2时，函数最小值为-8
点评：本题考查向量加减混合运算及几何意义，属基础题．
练习册系列答案
相关题目

指出下列各组命题中，p是q的什么条件(在“充分而不必要条件”，“必要而不充分条件”，“充要条件”，“既不充分又不必要条件”中选出一种作答)．

(1)在△ABC中，p：A＞B，q：BC＞AC；

(2)对于实数x，y，p：x＋y≠8，q：x≠2或y≠6；

(3)在△ABC中，p：sinA＞sinB，q：tanA＞tanB；

(4)已知x，y∈R，p：(x－1)2＋(y－2)2＝0，q：(x－1)(y－2)＝0．

指出下列各组命题中，p是q的什么条件？(在“充分而不必要条件”“必要而不充分条件”“充要条件”“既不充分也不必要条件”中选出一种)

(1)在△ABC中，p：∠A＞∠B，q：BC＞AC；

(2)p：a＝3，q：(a＋2)(a－3)＝0；

(3)p：a＞2，q：a＞5；

(4)p：a＜b，q：．
指出下列各组命题中，p是q的什么条件？（在“充分而不必要条件”“必要而不充分条件”“充要条件”“既不充分也不必要条件”中选出一种）

(1)在△ABC中，p:∠A＞∠B,q:BC＞AC;

(2)p:a=3,q:(a+2)(a-3)=0;

(3)p:a＞2,q:a＞5;

(4)p:a＜b,q:＜1.

指出下列各组命题中，p是q的什么条件？

(1)在△ABC中，p：A＞B，q：BC＞AC；

(2)p：a=3，q：(a+2)(a-3)=0；

(3)p：a＜b，q：＜1.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网