题目内容
函数f（x）=2x-tanx在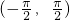
上的图象大致为
- A.
- B.
- C.
- D.
C
分析：由题意判断函数的奇偶性以及函数在x大于0时的单调性即可推出正确结果．
解答：因为函数f（x）=2x-tanx在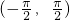上满足f（-x）=-f（x），所以函数是奇函数，
故A，B不正确；
又x=
→0+，函数f（x）=2×-tan=
＞0，
故C正确，D不正确．
故选C．
点评：本题考查函数的奇偶性与函数的单调性的应用，特值法是解答选择题的好方法．
分析：由题意判断函数的奇偶性以及函数在x大于0时的单调性即可推出正确结果．
解答：因为函数f（x）=2x-tanx在
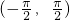上满足f（-x）=-f（x），所以函数是奇函数，故A，B不正确；
又x=
→0+，函数f（x）=2×-tan=＞0，故C正确，D不正确．
故选C．
点评：本题考查函数的奇偶性与函数的单调性的应用，特值法是解答选择题的好方法．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
设函数f（x）=
，则满足f（x）=4的x的值是（ ）
|
| A、2 | B、16 |
| C、2或16 | D、-2或16 |