题目内容
19.已知函数f(x)=2lnx+$\frac{{x}^{2}}{2}$+(5-m)x在(2,3)上单调递增,则m的取值范围为( )| A. | (-∞,5+2$\sqrt{2}$] | B. | (-∞,8] | C. | [$\frac{26}{3}$,+∞) | D. | (-∞,5+2$\sqrt{2}$) |
分析 求出函数的导数,问题转化为m-5≤$\frac{2}{x}$+x在(2,3)恒成立,令g(x)=x+$\frac{2}{x}$,x∈(2,3),根据函数的单调性求出m的范围即可.
解答 解:f′(x)=$\frac{2}{x}$+x+(5-m),
若f(x)在(2,3)递增,
则f′(x)≥0在(2,3)恒成立,
即m-5≤$\frac{2}{x}$+x在(2,3)恒成立,
令g(x)=x+$\frac{2}{x}$,x∈(2,3),
则g′(x)=1-$\frac{2}{{x}^{2}}$>0,
g(x)在(2,3)递增,
故g(x)>g(2)=3,
故m-5≤3,解得:m≤8,
故选:B.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及转化思想,是一道中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.在平面直角坐标系xOy中,已知O(0,0),A($\frac{15}{4}$,0),曲线C上任一点M满足|OM|=4|AM|,点P在直线y=$\sqrt{2}$(x-1)上,如果曲线C上总存在两点到点P的距离为2,那么点P的横坐标t的范围是( )
| A. | 1<t<3 | B. | 1<t<4 | C. | 2<t<3 | D. | 2<t<4 |
7.已知函数f(x)=tan(2x+$\frac{π}{3}$),则下列说法正确的是( )
| A. | f(x)在定义域是增函数 | B. | f(x)的对称中心是($\frac{kπ}{4}$-$\frac{π}{6}$,0)(k∈Z) | ||
| C. | f(x)是奇函数 | D. | f(x)的对称轴是x=$\frac{kπ}{2}$+$\frac{π}{12}$(k∈Z) |
 中,底面
中,底面 是边长为1的正方形,
是边长为1的正方形, ,
,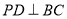 ,且
,且 ,
, 为
为 的中点.
的中点.
 平面
平面 ;
; 与平面
与平面 所成角的正弦值.
所成角的正弦值.