题目内容
6．已知曲线C1：$\left\{\begin{array}{l}x=12cosθ\\ y=4sinθ\end{array}\right.$（参数θ∈R），以坐标原点O为极点，x轴的非负半轴为极轴，建立极坐标系，曲线C2的极坐标方程为$ρ=\frac{3}{{cos（θ+\frac{π}{3}）}}$，点Q的极坐标为$（4\sqrt{2}，\frac{π}{4}）$．（1）将曲线C2的极坐标方程化为直角坐标方程，并求出点Q的直角坐标；
（2）设P为曲线C1上的点，求PQ中点M到曲线C2上的点的距离的最小值．
分析 （1）利用极坐标方程与直角坐标方程互化的方法，可得结论；
（2）利用参数方程，结合三角函数知识，求PQ中点M到曲线C2上的点的距离的最小值．
解答 解：（1）$ρ=\frac{3}{{cos（θ+\frac{π}{3}）}}$，得$\frac{1}{2}ρcosθ-\frac{{\sqrt{3}}}{2}ρsinθ=3$，
故曲线C2的直角坐标方程为$x-\sqrt{3}y-6=0$，
点Q的直角坐标为（4，4）．
（2）设P（12cosθ，4sinθ），故PQ中点M（2+6cosθ，2+2sinθ），C2的直线方程为$x-\sqrt{3}y-6=0$，
点M到C2的距离$d=\frac{{|2+6cosθ-\sqrt{3}（2+2sinθ）-6|}}{2}$=$|3cosθ-\sqrt{3}sinθ-2-\sqrt{3}|$
=$|2\sqrt{3}cos（θ+\frac{π}{6}）-2-\sqrt{3}|≥|2\sqrt{3}-2-\sqrt{3}|=2-\sqrt{3}$，
PQ中点M到曲线C2上的点的距离的最小值是$2-\sqrt{3}$．
点评 本题考查极坐标方程与直角坐标方程互化，考查参数方程的运用，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
1．执行如图所示的程序框图，如果输出T=6，那么判断框内应填入的条件是（ ）
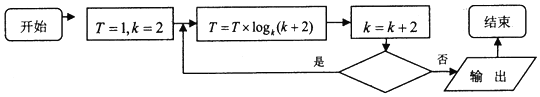
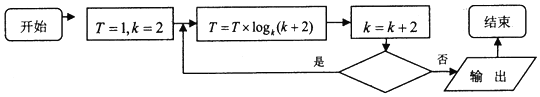
| A． | k＜32 | B． | k＜33 | C． | k＜64 | D． | k＜65 |
11．设F1，F2分别为椭圆C1：$\frac{x^2}{{{a_1}^2}}+\frac{y^2}{{{b_1}^2}}=1（{a_1}＞{b_1}＞0）$与双曲线C2：$\frac{x^2}{{{a_2}^2}}-\frac{y^2}{{{b_2}^2}}=1（{a_2}＞0，{b_2}＞0）$的公共焦点，它们在第一象限内交于点M，∠F1MF2=90°，若椭圆的离心率${e_1}=\frac{3}{4}$，则双曲线C2的离心率e2的值为（ ）
| A． | $\frac{9}{2}$ | B． | $\frac{{3\sqrt{2}}}{2}$ | C． | $\frac{3}{2}$ | D． | $\frac{5}{4}$ |
18．在如图所示的程序图中，若函数f（x）=$\left\{\begin{array}{l}{{2}^{x}，αx≤0}\\{lo{g}_{\frac{1}{2}}x，x＞0}\end{array}\right.$，则输出的结果是（ ）
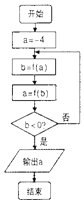
| A． | -3 | B． | $\frac{1}{16}$ | C． | $\frac{1}{4}$ | D． | 4 |