题目内容
已知△ABC的三边分别为AB=5,BC=4,AC=3,M是AB边上一点,P是平面ABC外一点,给出下列四个命题:
(1)若PA⊥平面ABC,则三棱锥P-ABC的四个面都是直角三角形;
(2)若PM⊥平面ABC,M是AB边上中点,则有PA=PB=PC;
(3)若PC=5,P在平面ABC上的射影是△ABC内切圆的圆心,则点P到平面ABC是的距离为
;
(4)若PC=5,PC⊥平面ABC,则△PCM面积的最小值为
.
其中正确命题的序号为 .
(1)若PA⊥平面ABC,则三棱锥P-ABC的四个面都是直角三角形;
(2)若PM⊥平面ABC,M是AB边上中点,则有PA=PB=PC;
(3)若PC=5,P在平面ABC上的射影是△ABC内切圆的圆心,则点P到平面ABC是的距离为
| 23 |
(4)若PC=5,PC⊥平面ABC,则△PCM面积的最小值为
| 15 |
| 2 |
其中正确命题的序号为
考点:点、线、面间的距离计算
专题:空间位置关系与距离
分析:由已知易得AC⊥BC,(1)由线面垂直可判BC⊥平面PAC,可证△PBC为直角三角形,其它3个是明显的;
(2)可得可得MA、MB、MC分别为PA、PB、PC在平面ABC内的摄影线段,易判相等;
(3)由等面积可求得内切圆的半径r=1,由勾股定理可得点P到平面ABC是的距离d=2
;
(4)当CM取最小值时,△PCM面积取最小值,由等面积可求得CM=
,可得△PCM面积S=6
(2)可得可得MA、MB、MC分别为PA、PB、PC在平面ABC内的摄影线段,易判相等;
(3)由等面积可求得内切圆的半径r=1,由勾股定理可得点P到平面ABC是的距离d=2
| 6 |
(4)当CM取最小值时,△PCM面积取最小值,由等面积可求得CM=
| 12 |
| 5 |
解答:
解:∵△ABC的三边分别为AB=5,BC=4,AC=3,
∴BC2+AC2=AB2,∴∠ACB=90°,即AC⊥BC,
(1)若PA⊥平面ABC,易得△ABC,△PAB,△PAC均为直角三角形,
对于△PBC,由PA⊥平面ABC可得PA⊥BC,又AC⊥BC,故BC⊥平面PAC,
可得BC⊥PC,故△PBC也为直角三角形,
∴三棱锥P-ABC的四个面都是直角三角形,故正确;
(2)若M是AB边上中点,则有MA=MB=MC,
再由PM⊥平面ABC可得MA、MB、MC分别为PA、PB、PC在平面ABC内的摄影线段,
∵必有PA=PB=PC,故正确;
(3)若PC=5,P在平面ABC上的射影是△ABC内切圆的圆心,
则点P到平面ABC是的距离d与内切圆半径r满足d2+r2=PC2,
由等面积可得
×3×4=
r(3+4+5),解得r=1
∴点P到平面ABC是的距离d=
=2
,不是
,故错误;
(4)若PC=5,PC⊥平面ABC,则当CM取最小值时,△PCM面积取最小值,
而当CM⊥AB时,CM取最小值,由等面积可得
×5×CM=
×3×4,
解得CM=
,此时△PCM面积S=
×5×
=6,不是
,故错误.
故答案为:(1)(2)
∴BC2+AC2=AB2,∴∠ACB=90°,即AC⊥BC,
(1)若PA⊥平面ABC,易得△ABC,△PAB,△PAC均为直角三角形,
对于△PBC,由PA⊥平面ABC可得PA⊥BC,又AC⊥BC,故BC⊥平面PAC,
可得BC⊥PC,故△PBC也为直角三角形,
∴三棱锥P-ABC的四个面都是直角三角形,故正确;
(2)若M是AB边上中点,则有MA=MB=MC,
再由PM⊥平面ABC可得MA、MB、MC分别为PA、PB、PC在平面ABC内的摄影线段,
∵必有PA=PB=PC,故正确;
(3)若PC=5,P在平面ABC上的射影是△ABC内切圆的圆心,
则点P到平面ABC是的距离d与内切圆半径r满足d2+r2=PC2,
由等面积可得
| 1 |
| 2 |
| 1 |
| 2 |
∴点P到平面ABC是的距离d=
| 52-12 |
| 6 |
| 23 |
(4)若PC=5,PC⊥平面ABC,则当CM取最小值时,△PCM面积取最小值,
而当CM⊥AB时,CM取最小值,由等面积可得
| 1 |
| 2 |
| 1 |
| 2 |
解得CM=
| 12 |
| 5 |
| 1 |
| 2 |
| 12 |
| 5 |
| 15 |
| 2 |
故答案为:(1)(2)
点评:本题考查空间线面位置关系,涉及线面垂直和射影以及等积法,属中档题.

练习册系列答案
相关题目
函数y=sin2x的图象经过适当变换可以得到y=cos2x的图象,则这种变换可以是( )
A、沿x轴向右平移
| ||
B、沿x轴向左平移
| ||
C、沿x轴向左平移
| ||
D、沿x轴向右平移
|
已知an=
(n∈N*),数列{an}的前项和为Sn,则使Sn>0的n最小值( )
| 3 |
| 2n-101 |
| A、99 | B、100 |
| C、101 | D、102 |
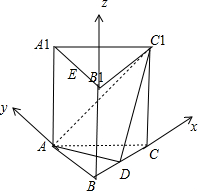 (理)如图,在直三棱柱ABC-A1B1C1中,AB=BC=2AA1=2,∠ABC=90°,D是BC的中点.
(理)如图,在直三棱柱ABC-A1B1C1中,AB=BC=2AA1=2,∠ABC=90°,D是BC的中点.