题目内容
18.海面上有A,B,C三个灯塔,AB=10nmile,$BC=5\sqrt{6}$nmile,从A望C和B成600视角,则从B望C和A成( )视角.| A. | 750 | B. | 450 | C. | 300 | D. | 150 |
分析 由题意抽象出△ABC,然后利用正弦定理求解.
解答 解:如图,
AB=10,BC=$5\sqrt{6}$,∠BAC=60°.
由正弦定理可得:$\frac{10}{sinC}=\frac{5\sqrt{6}}{sin60°}=\frac{5\sqrt{6}}{\frac{\sqrt{3}}{2}}=10\sqrt{2}$,
∴sinC=$\frac{\sqrt{2}}{2}$,
∵10$<5\sqrt{6}$,∴C=45°.
则∠ABC=180°-60°-45°=75°.
故从B望C和A成75°视角.
故选:A.
点评 本题考查了正弦定理在实际问题中的应用,理解题意,建立关系是解题的关键.属于基础题.

练习册系列答案
相关题目
6.已知向量$\overrightarrow{α}$,$\overrightarrow{β}$,$\overrightarrow{γ}$ 满足|$\overrightarrow{α}$|=1,$\overrightarrow{α}$⊥($\overrightarrow{α}$-2$\overrightarrow{β}$),($\overrightarrow{α}$-$\overrightarrow{γ}$)⊥($\overrightarrow{β}$-$\overrightarrow{γ}$),若|$\overrightarrow{β}$|=$\frac{\sqrt{17}}{2}$,|$\overrightarrow{γ}$|的最大值和最小值分别为m,n,则m+n等于( )
| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{5}{2}$ | D. | $\frac{{\sqrt{15}}}{2}$ |
13.若函数y=f(x)同时具有下列三个性质:(1)最小正周期为π;(2)在$x=\frac{π}{3}$时取得最大值1;(3)在区间$[{-\frac{π}{6},\frac{π}{3}}]$上是增函数.则y=f(x)的解析式可以是( )
| A. | $y=sin({\frac{x}{2}+\frac{π}{6}})$ | B. | $y=cos({2x+\frac{π}{3}})$ | C. | $y=sin({2x-\frac{π}{6}})$ | D. | $y=cos({2x-\frac{π}{6}})$ |
10.若sinα+sinβ+sinγ=0,cosα+cosβ+cosγ=0,且0≤α<β<γ<2π,则β-α=( )
| A. | $\frac{4π}{3}或\frac{2π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{4π}{3}$ | D. | 以上答案都不对 |
 中,内角
中,内角 ,
, ,
, 所对的边分别是
所对的边分别是 ,
, ,
, ,已知
,已知 ,
, ,则
,则 ( )
( ) B.
B.
 D.
D.
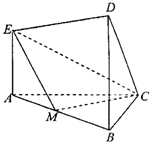 在如图所示的几何体中.EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,且AC=BC=BD=2AE=2,M是AB的中点.
在如图所示的几何体中.EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,且AC=BC=BD=2AE=2,M是AB的中点.