题目内容
曲线
在二阶矩阵
的作用下变换为曲线
，
（I）求实数
的值；
（II）求
的逆矩阵
.
（1）
；（2）
.
解析试题分析：（1）在曲线上分别设点，再利用矩阵变换找出两点坐标的关系，根据待定系数法求出的值，（2）因为
，则可以根据求逆矩阵的方法直接可以求出逆矩阵.
试题解析：
设
为曲线上任意一点，
为曲线上与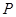
对应的点，则
，即
带入到得，
，化简得
那么就有
解得
（2）因为，故
考点：本题主要考查矩阵，矩阵与变换知识.
练习册系列答案
口算能手系列答案
相关题目
集合M={x|y=lgx}，集合N={y|y=10x}，则（ ）
| A、M∩N=φ | B、M∪N=R | C、M=N | D、M∩N={（1，1）} |
＝1在M－1的作用下的新曲线的方程．
， （1）求逆矩阵
；（2）若矩阵
满足
，试求矩阵
中，直线
在矩阵
对应的变换作用下得到直线
，求实数
、
的值．
对应的变换矩阵是
在
的坐标；
的图象在已知
、
、
是
的三边长，且满足
，则一定是（ ）．
| A．等腰非等边三角形 | B．等边三角形 |
| C．直角三角形 | D．等腰直角三角形 |
之下的对应点的坐标为(－2，－4)，求m、k的值．
.