题目内容
在平面直角坐标系
中，直线
在矩阵
对应的变换作用下得到直线
，求实数
、
的值．
，
.
解析试题分析：确定变换前的坐标
个变换后的坐标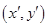
之间的关系，然后用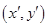坐标来表示坐标，并将上一步的结果代入直线
便可以得到一条直线方程，根据两者的系数关系求出、的值.
试题解析：设坐标在矩阵
的变换后的坐标为，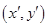
则有
，于是有
，解得
， 4分
将上述结果代入直线的方程得
，
化简得
，（*） 6分
于是有
，解得
或
， 8分
当
，
时，代入（*）式得
，不合乎题意，舍去！ 9分
综上所述，. 10分
考点：矩阵变换
练习册系列答案
名校课堂系列答案
相关题目
下列各组对象中，能构成集合的是（ ）
（1）比较小的正整数的全体；（2）一切很大的数；（3）自然数；（4）正三角形的全体．
（1）比较小的正整数的全体；（2）一切很大的数；（3）自然数；（4）正三角形的全体．
| A、（1）（2） | B、（2）（3） | C、（1）（4） | D、（3）（4） |
，N＝
，试求曲线y＝sinx在矩阵MN变换下的曲线方程．
，若
=
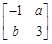所对应的变换TM把直线2x-y=3变换成自身，试求实数a，b．
在二阶矩阵
的作用下变换为曲线
，
的值；
的逆矩阵
.
有一个属于特征值1的特征向量
.
，求直线
先在矩阵A，再在矩阵B的对应变换作用下的像的方程. 
在矩阵
对应的变换下变成椭圆
求矩阵
的逆矩阵
.
的最小正周期
=____________．