题目内容

求证：≥ (a＞0,b＞0).

证法一：(分析法)要证≥，

只要证a+b≥a+b，

即证≥.

需证(+)(a-+b)≥，

即a-+b≥，

也就是要证a+b≥2成立.a+b≥2显然成立，∴原不等式成立.

证法二：(综合法)∵a、b为正实数，

∴a+b≥2.

又≥2,                                                 ①

≥2，                                                  ②

①+②得≥，

即≥成立.

证法三：(作差比较法)

(

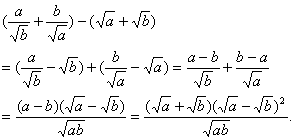
∵a、b为正实数，

∴＞0,＞0,()2≥0.

于是有≥0.

∴≥.

练习册系列答案
相关题目
已知函数f（x）在R上是增函数，a，b∈R．
（1）求证：如果a+b≥0，那么f（a）+f（b）≥f（-a）+f（-b）；
（2）判断（1）中的命题的逆命题是否成立？并证明你的结论；解不等式f(lg
1-x
1+x
)+f(2)≥f(lg
1+x
1-x
)+f(-2)．
已知函数f（x）=2x+alnx．
（1）若f（x）在[1，+∞）上为增函数，求a的范围；
（2）求证：若a＜0，对于任意两个正数x1、x2总有：
f(x1)+f(x2)
2
≥f(
x1+x2
2
)
（3）若存在x∈[1，e]，使不等式f（x）≤（a+3）x-
1
2
x2成立，求实数a的取值范围．
设函数f（x）的定义域为R，若|f（x）|≤|x|对一切实数x均成立，则称函数f（x）为Ω函数．
（Ⅰ）试判断函数f1（x）=xsinx、f2（x）=
e-x
ex+1
和f3（x）=
x2
x2+1
中哪些是Ω函数，并说明理由；
（Ⅱ）若函数y=f（x）是定义在R上的奇函数，且满足对一切实数x1、x2，均有|f（x1）-f（x2）|≤|x1-x2|，求证：函数f（x）一定是Ω函数；
（Ⅲ）求证：若a＞0，则函数f（x）=ln（x2+a）-lna是Ω函数．
定义在R上的函数，对任意x1，x2∈R，都有f(
x1+x2
2
)≥
1
2
[f(x1)+f(x2)]，则称函数f（x）是R上的凸函数．已知二次函数f（x）=ax2+x（a∈R，a≠0）．
（1）求证：当a＜0时，函数f（x）是凸函数；
（2）对任意x∈（0，1]，f（x）≥-1恒成立，求实数a的取值范围．
已知函数f（x）=ln（1+x）-x；
（I）求证：对?a＞0，f（x）≤ax2；
（II）证明：ln（n+1）≤
2
12
+
3
22
+
4
32
+…+
n+1
n2
，（n∈N*）；
（III）求证：对?t∈R，e2x-2t（ex+x）+x2+2t2-
1
2
≥0．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网