题目内容
18.已知函数f(x)的定义域为R,若存在常数k>0,使|f(x)|≤$\frac{k}{2016}$|x|对一切实数x均成立,则称f(x)为“期盼函数”.给出下列函数:①f(x)=x3;②f(x)=$\sqrt{3}$sinx+cosx;③f(x)=$\frac{x}{{x}^{2}+x+1}$;④f(x)=$\frac{x}{{2}^{x}+1}$
其中f(x)是“期盼函数”的有( )个.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据新定义,对每个函数一一验证,即可得出结论.
解答 解:①f(x)=x3,|f(x)|=|x3|≤$\frac{k}{2016}$|x|,即|x2|≤$\frac{k}{2016}$,不存在这样的k对一切实数x均成立,
②f(x)=$\sqrt{3}$sinx+cosx=2sin(x+$\frac{π}{6}$),|f(x)|=|2sin(x+$\frac{π}{6}$)|≤$\frac{k}{2016}$|x|,
x=0时,|f(x)|=1≤0,不成立;
③f(x)=$\frac{x}{{x}^{2}+x+1}$,则|f(x)|=|$\frac{x}{{x}^{2}+x+1}$|=$\frac{|x|}{{(x+\frac{1}{2})}^{2}+\frac{3}{4}}$≤$\frac{4}{3}$|x|,
故对任意的$\frac{k}{2016}$>$\frac{4}{3}$,都有|f(x)|<$\frac{k}{2016}$|x|,故③正确;
④f(x)=$\frac{x}{{2}^{x}+1}$,|f(x)|=$\frac{|x|}{{2}^{x}+1}$≤$\frac{k}{2016}$|x|,故④正确;
故选:B.
点评 本题主要考查学生的阅读理解能力.知识点方面主要考查了函数的最值及其几何意义,综合性较强.

练习册系列答案
 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
9.已知i是虚数单位,若1+i=z(1-i),则z=( )
| A. | -1 | B. | 1 | C. | -i | D. | i |
6.已知函数f(x)=sin($\frac{x}{2}$+$\frac{π}{4}$),则f($\frac{π}{2}$)=( )
| A. | -1 | B. | 1 | C. | -$\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
13.设F1,F2分别是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点,点M(3,$\sqrt{2}$)在此双曲线上,点F2到直线MF1的距离为$\frac{4\sqrt{6}}{9}$,则双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\frac{2\sqrt{6}}{3}$ |
3.偶函数f(x)定义在(-1,0)∪(0,1)上,且$f(\frac{1}{2})=0$,当x>0时,总有$(\frac{1}{x}-x)f'(x)•ln(1-{x^2})>2f(x)$,则不等式f(x)<0的解集为( )
| A. | {x|-1<x<1且x≠0} | B. | $\left\{x\right.|-1<x<-\frac{1}{2}$或$\frac{1}{2}<x<\left.1\right\}$ | ||
| C. | $\left\{{x|-\frac{1}{2}}\right.<x<\frac{1}{2}$且x≠0} | D. | {x|-1<x<-$\frac{1}{2}$或$0<x<\left.{\frac{1}{2}}\right\}$ |
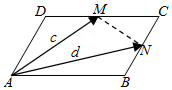 (1)如图,平行四边形ABCD中,M、N分别为DC、BC的中点,已知$\overrightarrow{AM}=\overrightarrow{c}$、$\overrightarrow{AN}=\overrightarrow{d}$,试用$\overrightarrow{c}$、$\overrightarrow{d}$表示$\overrightarrow{AB}$和$\overrightarrow{AD}$.
(1)如图,平行四边形ABCD中,M、N分别为DC、BC的中点,已知$\overrightarrow{AM}=\overrightarrow{c}$、$\overrightarrow{AN}=\overrightarrow{d}$,试用$\overrightarrow{c}$、$\overrightarrow{d}$表示$\overrightarrow{AB}$和$\overrightarrow{AD}$.