题目内容
若函数f(x)=|log2x|在区间(m,2m+1)(m>0)上不是单调函数,则实数m的取值范围是 .
分析:画出函数f(x)=|log2x|在区间(0,+∞)上的图象.由图象可等:若满足函数f(x)=|log2x|在区间(m,2m+1)(m>0)上不是单调函数,则必有1∈(m,2m+1).解出即可.
解答:解:画出函数f(x)=|log2x|在区间(0,+∞)上的图象.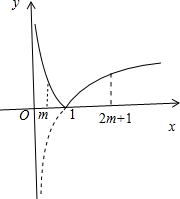
由图象可知:若满足函数f(x)=|log2x|在区间(m,2m+1)(m>0)上不是单调函数,
则必有1∈(m,2m+1).
∴
.
解得0<m<1.
∴实数m的取值范围是(0,1).
故答案为(0,1).

由图象可知:若满足函数f(x)=|log2x|在区间(m,2m+1)(m>0)上不是单调函数,
则必有1∈(m,2m+1).
∴
|
解得0<m<1.
∴实数m的取值范围是(0,1).
故答案为(0,1).
点评:本题考查了对数函数的图象与性质、含绝对值函数的图象的画法、函数的单调性等基础知识与基本技能,属于中档题.

练习册系列答案
相关题目