Question

利用函数的图象，指出下面函数零点所在的大致区间：

(1) f(x)=-x³-2x+1;         (2)f(x)=e^1+x+2x+2.

Answer 1

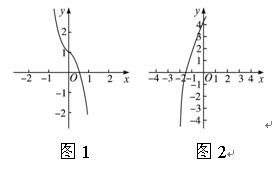
解析：（1）用计算器或计算机作出x、f(x)的对应值表（如下表）及其图象（如图1）.

x	-3	-2	-1	0	1	2	3
f(x)	34	13	4	1	-2	-11	-32

    由列表或图象可知，f(0)＞0，f(1)＜0，即f(0)·f(1)＜0，说明函数f(x)在区间(0,1)内有零点，且仅有一个.故函数f(x)的零点所在大致区间为（0，1）.

    （2）易知函数f(x)=e^1+x+2x+2在定义域R上是增函数.

    用图形计算器或计算机作出图象，如图2.

    由图象可知，f(-2)＜0，f(-1)＞0，即f(-2)·f(-1)＜0,说明函数在区间（-2，-1）内有零点，且仅有一个.故函数f(x)的零点所在大致区间为（-2，-1）.