题目内容
设f(x)是定义在R上的以3为周期的奇函数,若 f(1)>1,f(2015)=
,则实数a的取值范围是 .
| 2a-3 |
| a+1 |
考点:函数奇偶性的判断,函数的周期性
专题:计算题,函数的性质及应用,不等式的解法及应用
分析:先根据周期性和奇函数,将f(2015)化成f(-1)=-f(1),然后根据已知条件建立关系式,解分式不等式即可求出实数a的取值范围.
解答:
解:由f(x)是定义在R上的以3为周期的奇函数,
则f(x+3)=f(x),f(-x)=-f(x),
∴f(2015)=f(3×671+2)=f(2)=f(2-3)=f(-1)
=-f(1),
又f(1)>1,∴f(2015)<-1,
即
<-1,即为
<0,
即有(3a-2)(a+1)<0,解得,-1<a<
.
故答案为:(-1,
).
则f(x+3)=f(x),f(-x)=-f(x),
∴f(2015)=f(3×671+2)=f(2)=f(2-3)=f(-1)
=-f(1),
又f(1)>1,∴f(2015)<-1,
即
| 2a-3 |
| a+1 |
| 3a-2 |
| a+1 |
即有(3a-2)(a+1)<0,解得,-1<a<
| 2 |
| 3 |
故答案为:(-1,
| 2 |
| 3 |
点评:本题主要考查了函数的奇偶性与周期性的综合应用,周期性和奇偶性都是函数的整体性质,同时考查了分式不等式的求解,属于中档题.

练习册系列答案
相关题目
某算法的程序框图如图所示,如果输出的结果为26,则判断框内的条件应为( )


| A、k≤5? | B、k>4? |
| C、k>3? | D、k≤4? |
某工厂去年产值为a,计划今后5年内每年比上年产值增加10%,则从今年起到第5年,这个厂的总产值为( )
| A、1.14a |
| B、11×(1.15-1)a |
| C、1.15a |
| D、10×(1.16-1)a |
若θ∈(
,
),sin2θ=
则cosθ-sinθ的值是( )
| π |
| 4 |
| π |
| 2 |
| 1 |
| 16 |
A、
| ||||
B、
| ||||
C、-
| ||||
D、±
|
已知集合A={x|x<5},B={-1,3,5,7},则A∩B=( )
| A、{-1,3,5} |
| B、{-1,3} |
| C、{3,5} |
| D、{5,7} |
设曲线y=
在点(3,2)处的切线与直线ax+y+1=0垂直,则a=( )
| x+1 |
| x-1 |
| A、2 | ||
| B、-2 | ||
C、-
| ||
D、
|
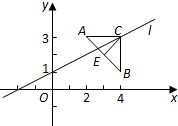 如图,已知点A(2,3),B(4,1),△ABC是以AB为底边的等腰三角形,点C在直线l:x-2y+2=0上.
如图,已知点A(2,3),B(4,1),△ABC是以AB为底边的等腰三角形,点C在直线l:x-2y+2=0上.